Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.
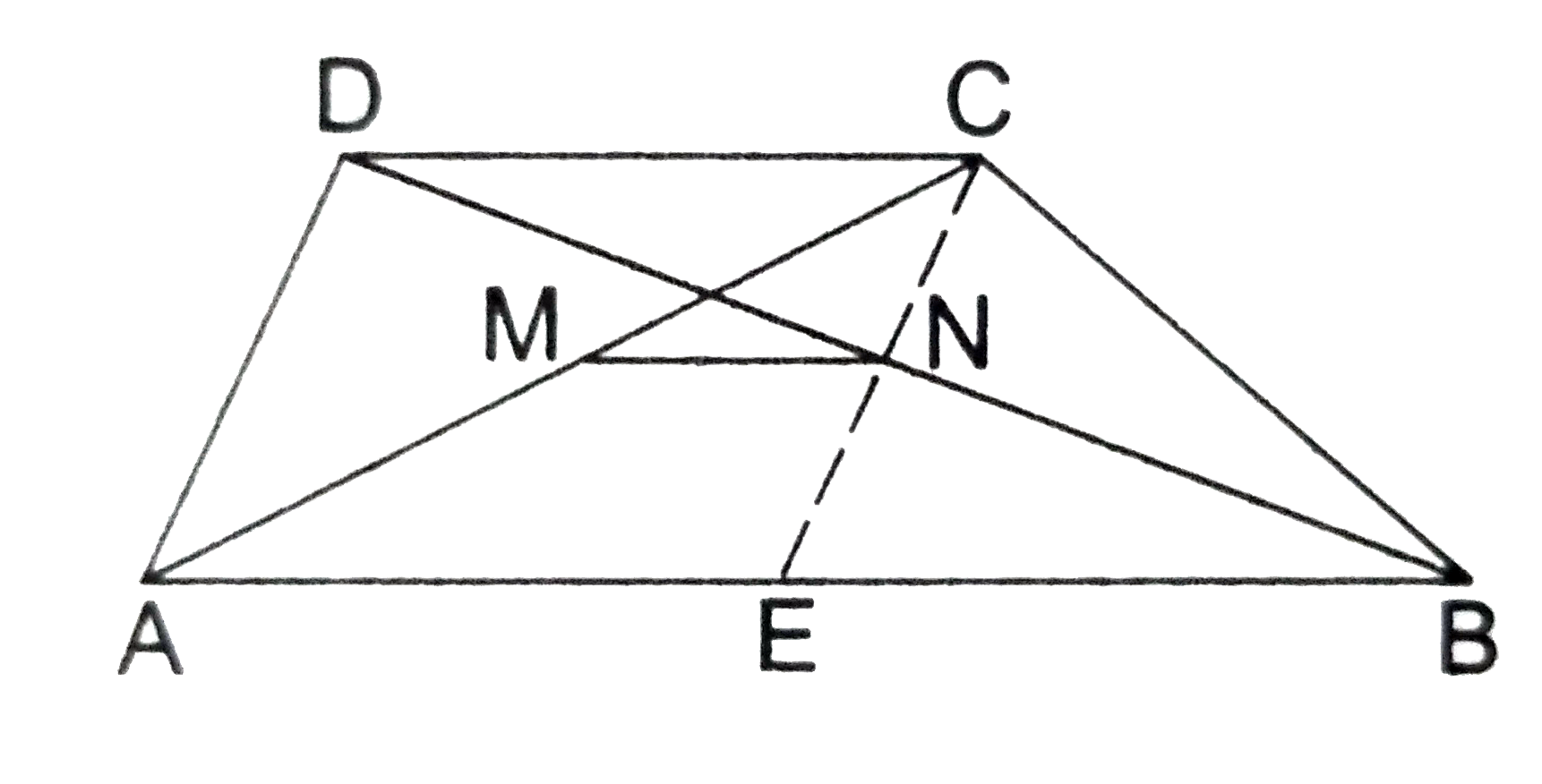
Let ABCD be a trapezium in which AB||DC, and let M and N be the midpoints of the diagonals AC and BD respectively.
Join CN and produce it to meet AB at E.
In △ CDN and EBN, we have:
DN=BN [∵ N is midpoint of BD]
∠DCN=∠BEN (alt,interior ∠)
∠CDN=∠EBN (alt. interior ∠)
∴△CDN≅△EBN [SAA-criterial].
∴DC=EBandCN=NE (c.p.c.t.).
Thus, in △CAE, the points M and N are the midpoints of AC and CE respectively.
∴MN||AE and MN=12AE⇒ MN||AB||DC
andMN=12AE=12(AB−EB)=12(AB−DC) [∵EB=DC].
Similar Questions
The line joining the mid points of the diagonals of a trapezium is parallel to each of the parallel sides and equal to half of their difference
View SolutionProve that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionProve that the segment joining the middle points of two non-parallel sides of a trapezium is parallel to the parallel sides and half of their sum.
View SolutionThe line joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionProve that the line segment joining the mid points of two sides of a triangle is parallel to its third side.
View SolutionExamples: Prove that the segment joining the middle points of two non parallel sides of a trapezium is parallel to the parallel sides and half of their sum.
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionThe line segment joining the mid-points of any two sides of a triangle in parallel to the third side and equal to half of it.
View Solution