Prove that the rectangle circumscribing a circle is a square
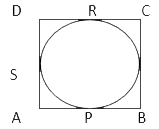
AP=AS,BP=BQ,CR=CQ andDR = DS
⇒AP+BP+CR+DR=AS+BQ+CQ+DS
Q⇒AB+CD=AD+CB
ButAB=CDandAD=CB
∴AB=AD
Hence,ABCD is a square.
Topper's Solved these Questions
- SAMPLE PAPER 2019Book:X BOARDSChapter:SAMPLE PAPER 2019Exercise:25A
Explore 1 Video
- SAMPLE PAPER 2019Book:X BOARDSChapter:SAMPLE PAPER 2019Exercise:25B
Explore 1 Video
- SAMPLE PAPER 2019Book:X BOARDSChapter:SAMPLE PAPER 2019Exercise:Section – B
Explore 1 Video
- QUESTION PAPER 2023Book:X BOARDSChapter:QUESTION PAPER 2023Exercise:Question
Explore 88 Videos
- X BoardsBook:X BOARDSChapter:X BoardsExercise:All Questions
Explore 494 Videos
Similar Questions
Prove that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionShow that the rectangle of maximum area that can be inscribed in a circle is a square.
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View SolutionShow that the rectangle of maximum area that can be inscribed in a circle is a square.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
View SolutionABCD is a square in first quadrant whose side is a, taking ABandAD as axes, prove that the equation to the circle circumscribing the square is x2+y2=a(x+y).
View SolutionShow that of all the rectangles inscribed in a given circle, the square has the maximum area.
View SolutionWill it be true to say that the perimeter of a square circumscribing a circle of radius a cm is 8a cm ? Give reson for your answer.
View SolutionFind the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x?
View Solution