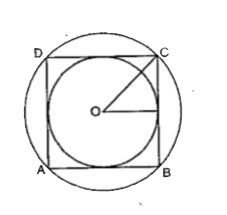
Prove that the rectangle circumscribing a circle is a square
Step by step video solution for Prove that the rectangle circumscribing a circle is a square by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If the area of region bounded by the inscribed and circumscribed circles of a square is 9π, then the area of the square will be :
 A6πB5πC25D36
A6πB5πC25D36
Show that the rectangle of maximum area that can be inscribed in a circle is a square.
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View SolutionShow that the rectangle of maximum area that can be inscribed in a circle is a square.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
View SolutionABCD is a square in first quadrant whose side is a, taking ABandAD as axes, prove that the equation to the circle circumscribing the square is x2+y2=a(x+y).
View SolutionShow that of all the rectangles inscribed in a given circle, the square has the maximum area.
View SolutionWill it be true to say that the perimeter of a square circumscribing a circle of radius a cm is 8a cm ? Give reson for your answer.
View Solution
