show that the tangents to thre curve y=2x3−3 at the point where x=2 and x=-2 are parallel
The correct Answer is:A, B, C, D
a. Area =2(121×1)=1 sq. units.

b. y2=x3and|y|=2x, both the curve are symmetric about y-axis

4x2=x3orx=0,4.
Required area =24∫0(2x−x3/2)dx=325 sq. units.
c. √x+√|y|=1
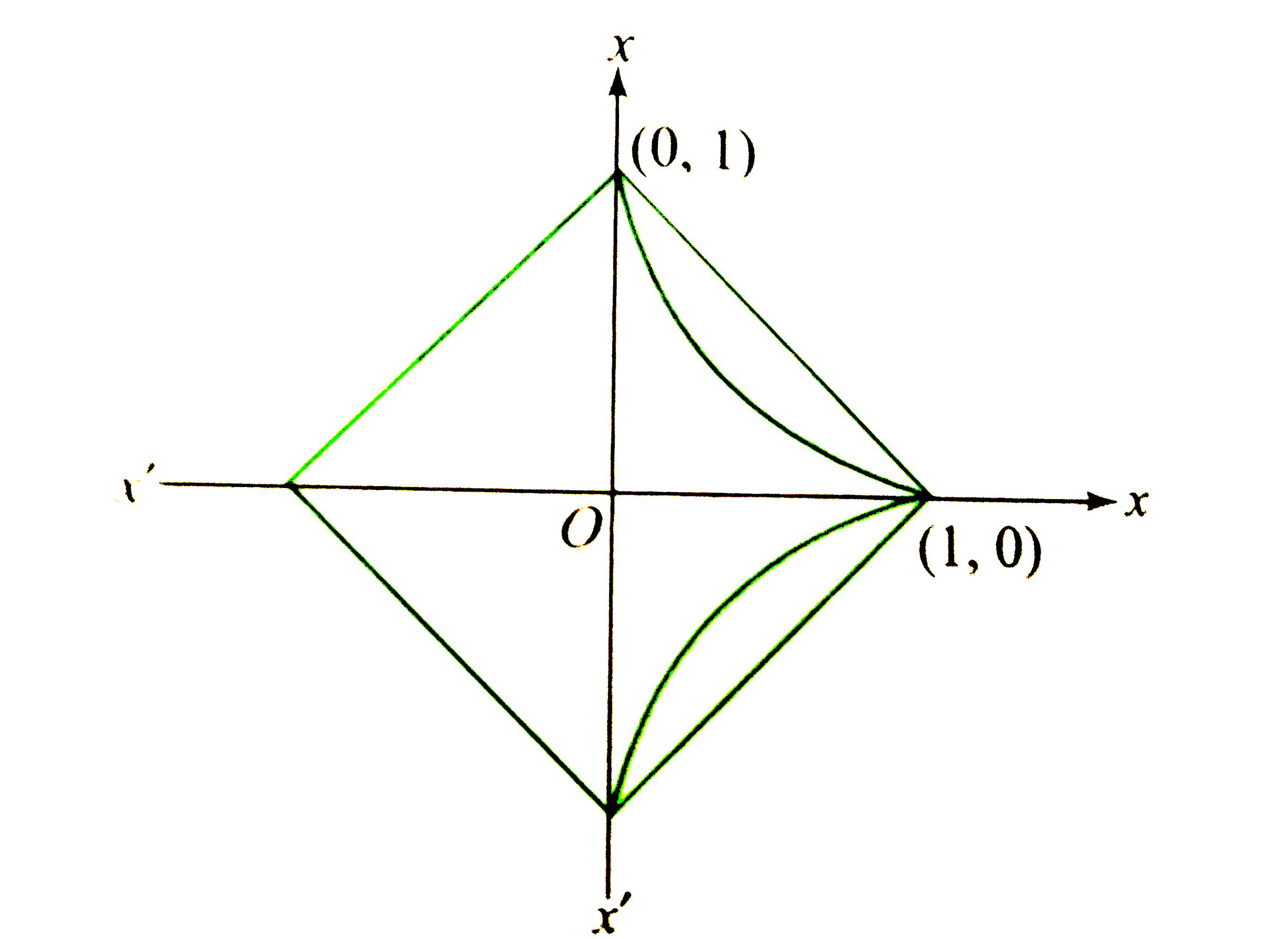
The curve is symmetrical about x-axis
√|y|=1−√xand√x=1−√|y|
⇒ for x>0,y>0√y=1−√x
12√ydydx=−12√x
dydx=−√yx
dydx<0, function is decreasing
Required area =21∫0((1−x)−(1−2√x+x))dx
=41∫0(√x−x)dx
=4[x3/23/2−x22]10
=4[23−12]
=23 sq. units.
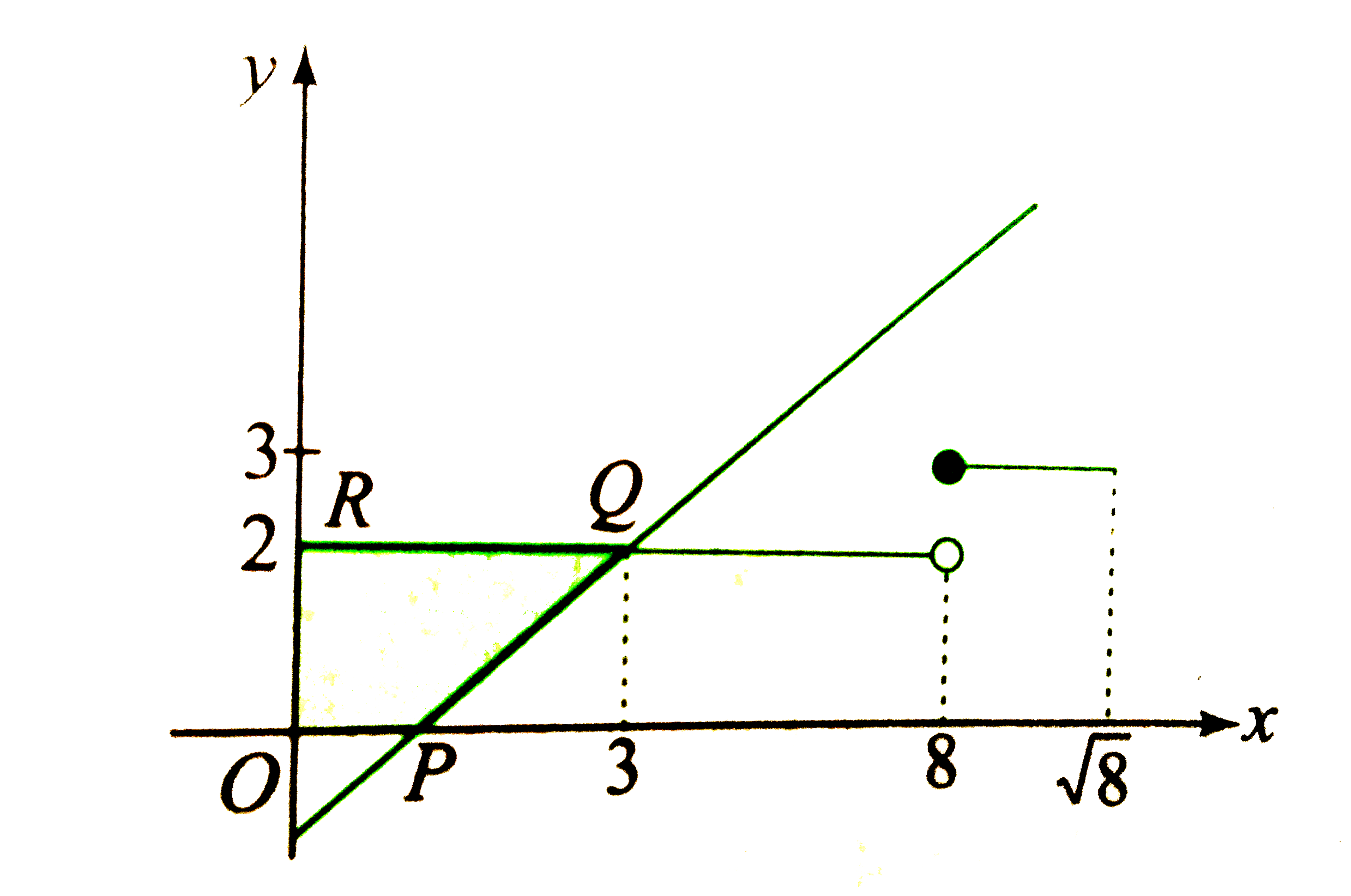
d. If −8<x<8, then y=2.
If x∈(−8√2,−8]∪[8,8√2), then y=3, and so on
Intersection of y=x−1andy=2. We get x=3∈(−8,8).
Intersection of y=x−1andy=3.
We get x=4∉(−8√2,−8]∪[8,8√2).
Similarly, y=x−1 will not intersect y=[x264+2] at any
other integral, except in the interval x∈(−8,8).
Required area (shaded region ) =2×3−12×2×2
=4 sq. units.
Topper's Solved these Questions
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Numerical Value Type
Explore 18 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Archives
Explore 10 Videos
- AREABook:CENGAGE ENGLISHChapter:AREAExercise:Linkded Comprehension Type
Explore 21 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
Similar Questions
Show that the tangents to the curve y=2x3−3 at the points where x=2 and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=x3−3 at the points where x=2and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=7x3+11 at the points where x=2 and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=7x3+11 at the points x=2 and x=−2 are parallel.
View SolutionProve that the tangents to the curve y=x2−5x+6 at the points (2, 0) and (3, 0) are at right angles.
View SolutionThe slope of the tangent to the curve y=x2−x at the point where the line y = 2 cuts the curve in the first quadrant, is
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionWrite the equation of the tangent to the curve y=x2−x+2 at the point where it crosses the y-axis.
View SolutionFind the equation of the tangent to the curve y=x−7(x−2)(x−3) at the point where it cuts the x-axis.
View Solution
