Sides of two similar triangles are in the ratio 4:9 . Areas of these triangles are in the ratio. 2:3 (b) 4:9 (c) 81:16 (d) 16:81
2:3
4:9
81:16
16:81
Step by step video & image solution for Sides of two similar triangles are in the ratio 4:9 . Areas of these triangles are in the ratio. 2:3 (b) 4:9 (c) 81 : 16 (d) 16 : 81 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - UNIQUE PUBLICATIONCHAPTER - SIMILARITYEXERCISE - Unique practise Session (1 Marks Question)
3 Videos
- SIMILARITYBOOK - UNIQUE PUBLICATIONCHAPTER - SIMILARITYEXERCISE - Unique practise Session (2 Marks Question)
2 Videos
- SIMILARITYBOOK - UNIQUE PUBLICATIONCHAPTER - SIMILARITYEXERCISE - Assignment-I
5 Videos
- QUADRATIC EQUATIONS BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT
6 Videos
- STATISTICS BOOK - UNIQUE PUBLICATIONCHAPTER - STATISTICS EXERCISE - PROBLEM SET
6 Videos
Similar Questions
SAS Similarity Criterion : If in two triangle; one pair of corresponding sides are proportional and the included angles are equal then two triangles are similar.
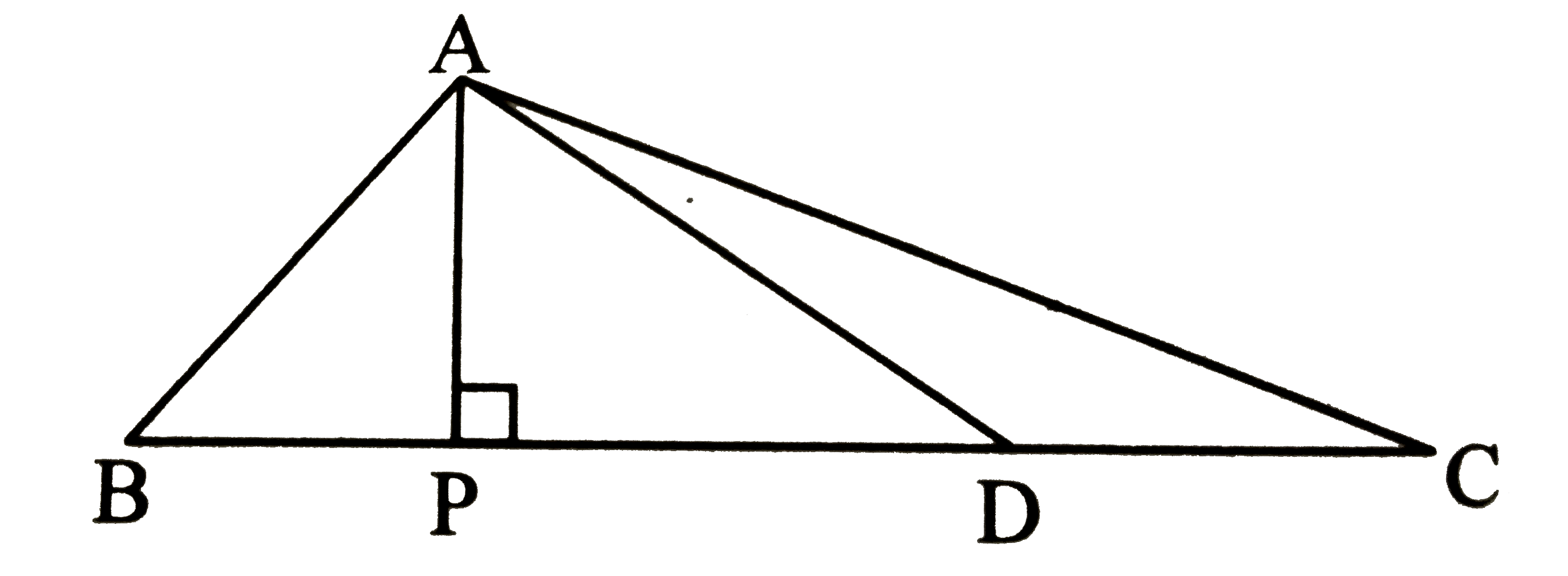
View SolutionIn ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
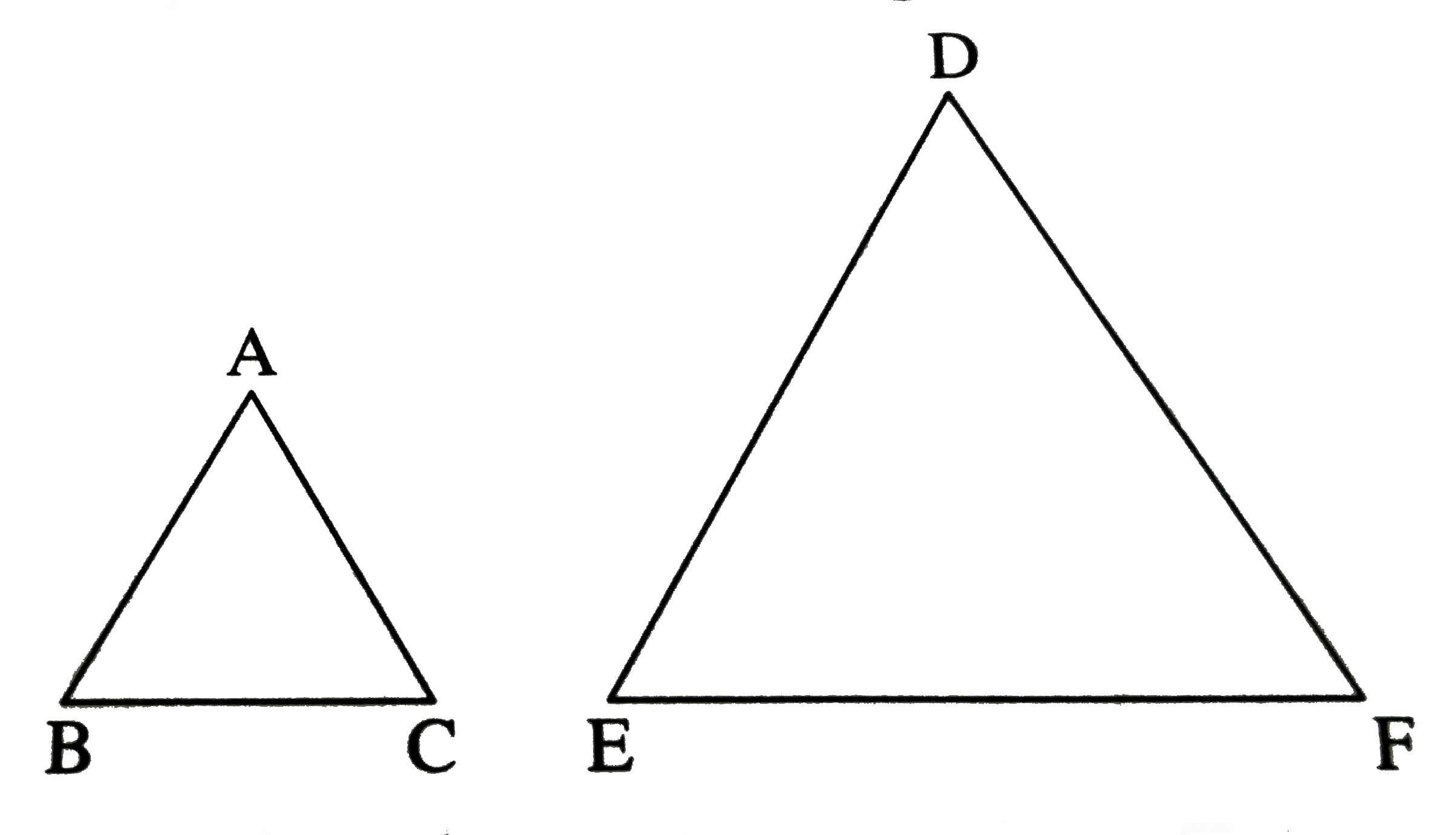
View SolutionΔABC and ΔDEF are equilateral triangles, A(ΔABC):A(ΔDEF)=1:2
If AB=4 then what is length of DE?
View SolutionOut of the following equations which one is nota quadratic equation ?
View SolutionThe person of O-blood group are 40% . The classification of person based on blood groups is to be shown by pie diagram . What should be the measures of angle for the persons of O-blood group ?
View SolutionTick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid point of BC Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2:3 (B) 4:9 (C) 81:16 (D) 16:81
View SolutionQ.27 The ratio of the circumferences of two circles is 4:9 ,the ratio of the areas is (A) 2:3(B)16:81(C)9:4(D)81:16
View SolutionSides of two similar triangles are in the ratio 4:9 . Areas of these triangles are in the ratio. (a)2:3 (b) 4:9 (c) 81:16 (d) 16:81
Ans-D
View Solution√2581−19=? 23 (b) 49 (c) 1681 (d) 2581
View SolutionThe value of (32243)−4/5 is a. 49 b. 94 c. 1681 d. 8116
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16:81 है तो इनकी भुजाओ का अनुपात ज्ञात कीजिए |
View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
View SolutionThe ratio of the sides of two symmetric triangles is 4: 9 and the ratio of their sides is (A) 2: 3 (B) 4: 9 (C) 81:16 (D) 16: 81
View SolutionTick the correct answer and justify: Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2:3 (B) 4:9 (C) 81:16 (D) 16:81
View SolutionSides of two similar triangles are in the ratio 4:9 . Areas of these triangles are in the ratio. 2:3 (b) 4:9 (c) 81:16 (d) 16:81
View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
View Solution
