Solve: √3x2−2√2x−2√3=0
The correct Answer is:√6and−√23
To solve the quadratic equation √3x2−2√2x−2√3=0, we can follow these steps:
Step 1: Identify the coefficients
The equation is in the standard form ax2+bx+c=0, where:
- a=√3
- b=−2√2
- c=−2√3
Step 2: Calculate the product ac
We need to calculate ac:
ac=√3×(−2√3)=−6
Step 3: Find two numbers that multiply to ac and add to b
We need to find two numbers that multiply to −6 and add to −2√2. The numbers are −3√2 and √2 because:
−3√2×√2=−6and−3√2+√2=−2√2
Step 4: Rewrite the middle term
We can rewrite the equation by splitting the middle term:
√3x2−3√2x+√2x−2√3=0
Step 5: Factor by grouping
Now, we will group the terms:
(√3x2−3√2x)+(√2x−2√3)=0
Factoring out common terms:
√3x(x−√2)+√2(x−√3)=0
Step 6: Factor completely
We can factor this as:
(√3x+√2)(x−√2)=0
Step 7: Set each factor to zero
Now we set each factor to zero:
1. √3x+√2=0
2. x−√2=0
Step 8: Solve for x
From the first factor:
√3x=−√2⟹x=−√2√3=−√63
From the second factor:
x=√2
Final Solutions
Thus, the solutions to the equation are:
x=−√63andx=√2
The equation is in the standard form ax2+bx+c=0, where:
- a=√3
- b=−2√2
- c=−2√3
We need to calculate ac:
ac=√3×(−2√3)=−6
We need to find two numbers that multiply to −6 and add to −2√2. The numbers are −3√2 and √2 because:
−3√2×√2=−6and−3√2+√2=−2√2
We can rewrite the equation by splitting the middle term:
√3x2−3√2x+√2x−2√3=0
Now, we will group the terms:
(√3x2−3√2x)+(√2x−2√3)=0
Factoring out common terms:
√3x(x−√2)+√2(x−√3)=0
We can factor this as:
(√3x+√2)(x−√2)=0
Now we set each factor to zero:
1. √3x+√2=0
2. x−√2=0
From the first factor:
√3x=−√2⟹x=−√2√3=−√63
x=√2
Thus, the solutions to the equation are:
x=−√63andx=√2
Topper's Solved these Questions
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section- B
3 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 4BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - Section -C
8 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section -C
7 Videos
Similar Questions
Consider the frequency distribution of the heights of 60 students of a class :
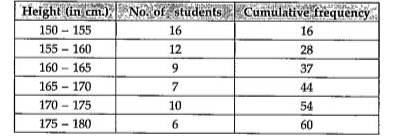
Find the sum of the lower limit of the modal class and the upper limit of the median class.
View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10)
View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10)
View SolutionA hemispherical depression is cut out from one face of a cubical block of side 7 cm such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. (Use π=227)
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).
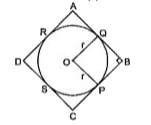
View SolutionSolve x2−(√3+1)x+√3=0.
View Solutionसमीकरण √3x2−√2x+3√3=0 को हल कीजिए।
View SolutionIf √2x=√√3+1√3−1, then x2−x= ______
View SolutionIf 0<x<π2 then solve cot2x−(√3+1)cotx+√3=0
View Solutionहल कीजिये tan2θ+(1−√3)tanθ−√3=0
View SolutionSolve tan2θ−(√3+1)tanθ+√3=0
View SolutionSolve for x by fractorisation
√3x2+10x+7√3=0
View SolutionSolve 4√3x2+5x−2√3=0
View SolutionSolve tan2θ+(1−√3)tanθ−√3=0
View SolutionSolve (2+√3)x2−2x+1+(2−√3)x2−2x−1=22−√3.
View SolutionSolve: √3x2+x+√3=0.
View Solution
