State whether the statements are true (T) or (F) false.
Diagonals of a rectangle are equal.
To determine whether the statement "Diagonals of a rectangle are equal" is true or false, we can follow these steps:
1. Understand the Definition of a Rectangle:
- A rectangle is a quadrilateral with opposite sides that are equal and all angles measuring 90 degrees.
2. Identify the Diagonals:
- A rectangle has two diagonals. These diagonals are the lines that connect opposite corners of the rectangle.
3. Use the Pythagorean Theorem:
- For any rectangle, if we denote the length as l and the breadth as b, the length of each diagonal can be calculated using the Pythagorean theorem.
- According to the theorem, the diagonal d can be calculated as:
d=√l2+b2
4. Calculate Both Diagonals:
- Since both diagonals connect the same pairs of opposite corners, they will both have the same length:
d1=√l2+b2
d2=√l2+b2
5. Compare the Diagonals:
- Since d1 and d2 are both equal to √l2+b2, we conclude that:
d1=d2
6. Conclusion:
- Therefore, the statement "Diagonals of a rectangle are equal" is True (T).
- A rectangle is a quadrilateral with opposite sides that are equal and all angles measuring 90 degrees.
- A rectangle has two diagonals. These diagonals are the lines that connect opposite corners of the rectangle.
- For any rectangle, if we denote the length as l and the breadth as b, the length of each diagonal can be calculated using the Pythagorean theorem.
- According to the theorem, the diagonal d can be calculated as:
d=√l2+b2
- Since both diagonals connect the same pairs of opposite corners, they will both have the same length:
d1=√l2+b2
d2=√l2+b2
- Since d1 and d2 are both equal to √l2+b2, we conclude that:
d1=d2
- Therefore, the statement "Diagonals of a rectangle are equal" is True (T).
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:APPLICATIONS, GAMES AND PUZZLES
Explore 3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:THINK AND DISCUSS
Explore 2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:THINK AND DISCUSS
Explore 2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBook:NCERT EXEMPLARChapter:SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTExercise:Exercise
Explore 52 Videos
- VISUALISING SOLID SHAPES Book:NCERT EXEMPLARChapter:VISUALISING SOLID SHAPES Exercise:EXERCISE
Explore 91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
Diagonals of rectangle bisect each other at right angles.
View SolutionState whether the statements are true (T) or (F) false.
Diagonals of a rhombus are equal and perpendicular to each other.
View SolutionState whether the statements are true (T) or (F) false.
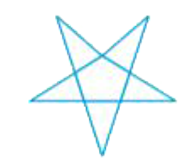 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
All angles of a trapezium are equal.
View SolutionState whether the statements are true (T) or (F) false.
If diagonals of a quadrilateral are equal, it must be a rectangle.
View SolutionState whether the statements are true (T) or (F) false.
All squares are rectangles.
View SolutionState whether the statements are true (T) or (F) false.
 is a concave pentagon.
is a concave pentagon.
View SolutionState whether the statements are true or falsea−b=b−a
View SolutionState whether the statements are true (T) or (F) false.
If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
View SolutionState whether the statements are true or falsea×b=b×a
View Solution