State whether the statements are true (T) or false (F).
The area of a trapezium become 4 times if its height gets doubled.
To determine whether the statement "The area of a trapezium becomes 4 times if its height gets doubled" is true or false, we can analyze the formula for the area of a trapezium.
1. Understand the Formula for the Area of a Trapezium:
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the two parallel sides, and h is the height.
2. Consider Doubling the Height:
If we double the height h, the new height becomes 2h. We can substitute this into the area formula:
A′=12×(a+b)×(2h)
3. Simplify the New Area:
Now, simplify the expression for the new area A′:
A′=12×(a+b)×2h=(a+b)×h
4. Relate the New Area to the Original Area:
The original area A was:
A=12×(a+b)×h
Now, we can see that:
A′=2×A
This means that when the height is doubled, the area becomes twice the original area, not four times.
5. Conclusion:
Therefore, the statement "The area of a trapezium becomes 4 times if its height gets doubled" is False.
Final Answer:
False (F)
The area A of a trapezium can be calculated using the formula:
A=12×(a+b)×h
where a and b are the lengths of the two parallel sides, and h is the height.
If we double the height h, the new height becomes 2h. We can substitute this into the area formula:
A′=12×(a+b)×(2h)
Now, simplify the expression for the new area A′:
A′=12×(a+b)×2h=(a+b)×h
The original area A was:
A=12×(a+b)×h
Now, we can see that:
A′=2×A
This means that when the height is doubled, the area becomes twice the original area, not four times.
Therefore, the statement "The area of a trapezium becomes 4 times if its height gets doubled" is False.
False (F)
Topper's Solved these Questions
- MENSURATIONBook:NCERT EXEMPLARChapter:MENSURATIONExercise:APPLICATIONS, GAMES AND PUZZLES
Explore 13 Videos
- MENSURATIONBook:NCERT EXEMPLARChapter:MENSURATIONExercise:THINK AND DISCUSS
Explore 2 Videos
- MENSURATIONBook:NCERT EXEMPLARChapter:MENSURATIONExercise:THINK AND DISCUSS
Explore 2 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBook:NCERT EXEMPLARChapter:LINEAR EQUATIONS IN ONE VARIABLEExercise:THINK AND DISCUSS
Explore 3 Videos
- PLAYING WITH NUMBERS Book:NCERT EXEMPLARChapter:PLAYING WITH NUMBERS Exercise:Think and Discuss
Explore 1 Video
Similar Questions
Rashid has decided to build a swimming pool as shown in the figure on an empty plot 25 metres long and 15 metres wide. He is discussing with his son Majid about his plan to build the pool, put tiles on the bottom of the pool and other requirements of the pool. Can you help Majid to answer the following questions which his father has asked in the discussion?

What is the surface area of the pool?
View SolutionA cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the piller at the rate of Rs10 per sq. m.
View SolutionA cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the piller at the rate of Rs10 per sq. m.
View SolutionSolve for x: 2x−53+x−32=16+2x
View SolutionWhat would be the value of y, if 277y is divisible by 11?
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View Solutionstate whether the statement are true (T) or false (F).
 is a simple closed curve.
is a simple closed curve.
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true (T) or (F) false.
All angles of a trapezium are equal.
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View SolutionState whether the statements are true (T) or (F) false.
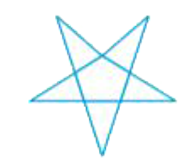 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
Rectangle is a regular quadrilateral.
View SolutionState whether the statements are true (T) or (F) false.
 is a concave pentagon.
is a concave pentagon.
View SolutionState whether the statements are true (T) or (F) false.
Every trapezium is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
Every parallelogram is a rectangle.
View SolutionState whether the statements are true (T) or (F) false.
Every trapezium is a rectangle.
View Solution