Statement (1) : If a and b are integers and roots of x2+ax+b=0 are rational then they must be integers. Statement (2): If the coefficient of x2 in a quadratic equation is unity then its roots must be integers
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:C
Let pq,(p,q∈Z,,q≠0andHCF(p,q)=1) be a root of x2+ax+b=0. Then, p2q2+apq+b=0
⇒ p2+apq+bq2=0
⇒ p2=−q(ap+bq)
⇒ qdividesp2 [∴qdivides-q(ap+bq)]
⇒ qdivides p [∴HCF(p,q)=1]
⇒ q=1 [∴HCF(p,q)=1]
Thus x2+ax+b=0 has integer roots.
So, statement-1 is true.
Statement-2 is false as x2+x+1=0 does not have integer roots.
Similar Questions
Knowledge Check
If the roots of x2−ax+b=0 are two consecutive odd integers, then a2−4b is equal to
A3B4C5D6If the roots of x2−bx+c=0 are two consecutive integers then b2−4c=
A1B2C3D4Statement -1 : A root of the equation (210−3)x2−211x+210+3=0 is 1
and
Statemen-2 : The sum of the coefficients of a quadratic equation is zero, then 1 is a root of the equation.AStatement -1 is True, Statement -2 is True, Statement -2 is a correct explanation for statement -10BStatement -1 is True, Statement -2 is True , Statement -2 is NOT a correct explanation for Statement -10CStatement -1 is True, Statement -2 is FalseDStatement -1 is Flase, Statement -2 is True
If a, b, c are distanct integers and w≠1 is a cube root of unity, then
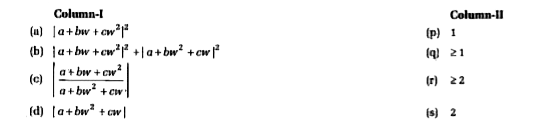
View SolutionIf the roots of x2−bx+c=0 are two consecutive integers then b2−4c=
View SolutionIf the roots of the equation x2−bx+c=0 are two consecutive integers then 3(b2−4c)=
View SolutionStatement 1: If a,b,c are all rational and one of the roots of the equation ax2+bx+c=0 is 2−√5 then the other root is 2+√5. Statement 2: In any quadratic equation with rational coefficients, the irrational roots always occur in the conjugate pair.
View SolutionThe roots of the equation x2+px+q=0 are consecutive integers. Find the discriminant of the quadratic equation.
View Solution

