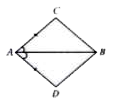
Suppose line segments AB and CD intersect at O in such a way that AO=OD and OB=OC. Prove that AC=BD but AC may not be parallel to BD
Step by step video solution for Suppose line segments A B\ a n d\ C D intersect at O in such a way that A O=O D\ a n d\ O B=O Cdot Prove that A C=B D but A C may not be parallel to B D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.1)
Explore 14 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.2)
Explore 9 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:OLYMPAID/ HOTS CORNER
Explore 10 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
In quadrilateral ABCD, AC=AD and AB bisects ∠A (see figure). Show that ΔABC≅ΔABD. What can you say about BC and BD ?
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionIf ΔABC is an obtuse angled triangle in which ∠C=110∘ then which one of the following is true ?
View SolutionThe weight (in kg) of 50 students are given below
40 45 55 62 50 51 56 69 61 36
60 56 69 38 35 63 57 50 57 48
40 63 53 64 47 42 56 51 42 60
55 39 64 57 64 44 66 35 59 59
73 62 49 63 37 63 54 72 44 60
Find the mean, median and mode respectively for the given data.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionSuppose line segments AB and CD intersect at O in such a way that AO=OD and OB=OC. Prove that AC=BD but AC may not be parallel to BD .
View SolutionIn Figure, line segment AB is parallel to another line segment CD . O is the mid-point of AD . Show that: (i)AOB≅DOC (ii)O is also the mid-point of BC.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD)=ar(△BOC) . Prove that ABCD is a trapezium.
View SolutionThe diagonals of quadrilateral ABCD intersect at O . Prove that ar(ACB)ar(ACD)=BODO
View SolutionIn Figure, given that ∠AOC=∠ACO and ∠BOD=∠BDO. Prove that AC∣∣DB
View SolutionSuppose line segments AB and CD intersect at O in such a way that AO=OD and OB=OC. Prove that AC=BD but AC may not be parallel to BD.
View SolutionTwo lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC.
View Solution