Tangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
The correct Answer is:(2,−2) or (-2,2)
cosθ=2√24=1√2
θ=45∘
∴A≡(2,2)
Let B≡(x1,y1)
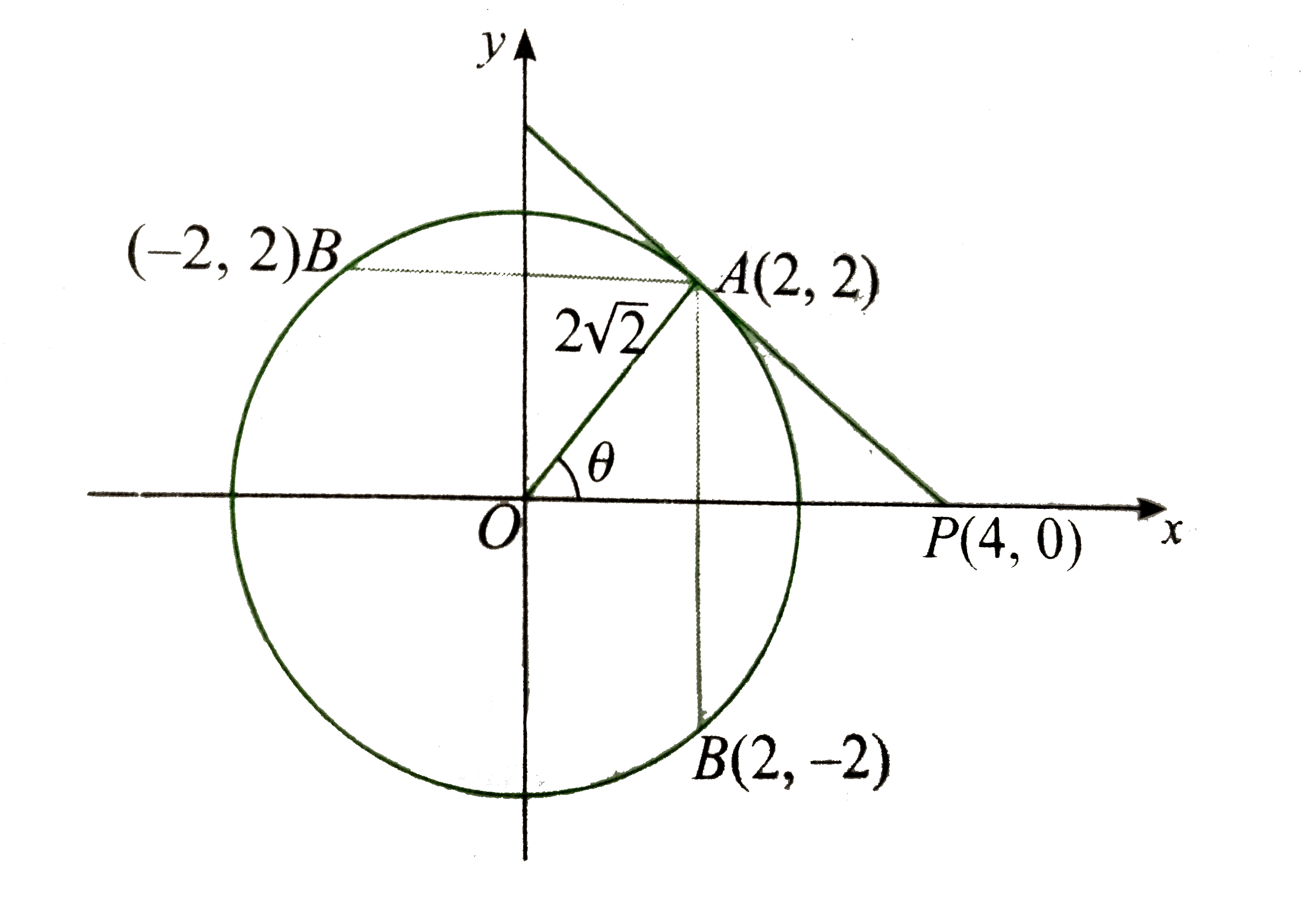
Given AB =4 . Therefore,
(x1−2)2+(y1−2)2=16
or x21+y21−4x1−4y1=8
Also, x21+y21=8
∴x1+y1=0
∴2x21=8
or x1±2
∴B≡(2,−2) or (−2,2)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.8
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.9
5 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.6
6 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
If the line x+2by+7=0 is a diameter of the circle x2+y2−6x+2y=0 , then find the value of b.
View SolutionFind the length of intercept, the circle x2+y2+10x−6y+9=0 makes on the x-axis.
View SolutionIf one end of the diameter is (1, 1) and the other end lies on the line x+y=3 , then find the locus of the center of the circle.
View SolutionConsider set A={T(r+1)=.nCr(3)n−r(5x)r,r=0,1,23,…..,n}. Match the following lists :

View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Area of triangle OPR when θ=π/4 is
View SolutionTangent drawn from the point P(4,0) to the circle x2+y2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that AB=4 .
View SolutionTangents drawn from the point P(1,8) to the circle x^(2)+y^(2)-6x-4y-11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then IRJ-
View SolutionTangents are drawn from P(3,0) to the circle x^(2)+y^(2)=1 touches the circle at points A and B.The equation of locus of the point whose distances from the point P and the line AB are equal is
View SolutionIf chord of contact of the tangent drawn from the point (a,b) to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 touches the circle x^(2)+y^(2)=k^(2), then find the locus of the point (a,b).
View SolutionTangents are drawn from a point P on the line y=4 to the circle x^(2)+y^(2)=25 .If the tangents are perpendicular to each other,then coordinates of P are
View SolutionThe tangents PA and PB are drawn from any point P of the circle x2+y2=2a2 to the circle x2+y2=a2. The chord of contact AB on extending meets again the first circle at the points A' and B'. The locus of the point of intersection of tangents at A' and B' may be given as
View SolutionIf a tangnet drawn from the point (4,0) to the circle x2+y2=8 touches it at a point A in the first quadrant, then the coordinates of another point B on the circle such that AB=4 are
View SolutionA tangent drawn from the point (4,0) to the circle x2+y2=8 touches it at a point A in the first quadrant. Find the coordinates of another point Bon the circle such that AB=4.
View Solutionchord of contact of the tangents drawn from a point on the circle x2+y2=81 to the circle x2+y2=b2 touches the circle x2+y2=16, then the value of b is
View SolutionTangents drawn from the point P (1, 8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solutionपरवलय y2=4x के उस बिंदु जहाँ यह वृत्त x2+y2=5 को प्रथम चतुर्थाश में काटता है, पर खींची गई स्पर्श रेखा बिंदु से होकर जाती है, वह है
View Solution

