The 4th term of an A.P. is equal to 3 times the first term and 7th term excess with the 3rd term by 1. Find its nth term.
The correct Answer is:18(2n+1)
To solve the problem, we need to find the nth term of an arithmetic progression (A.P.) given certain conditions about its terms. Let's break down the solution step by step.
Step 1: Understand the nth term of an A.P.
The nth term of an A.P. is given by the formula:
Tn=A+(n−1)D
where:
- A is the first term,
- D is the common difference,
- n is the term number.
Step 2: Set up the equations based on the given conditions.
1. The 4th term is equal to 3 times the first term:
T4=3A
Using the formula for the 4th term:
T4=A+3D
Therefore, we have:
A+3D=3A
Rearranging gives us:
3D=3A−A⟹3D=2A⟹A=3D2(Equation 1)
2. The 7th term exceeds the 3rd term by 1:
T7=T3+1
Using the formulas for the 7th and 3rd terms:
T7=A+6DandT3=A+2D
Therefore, we have:
A+6D=(A+2D)+1
Simplifying gives:
A+6D=A+2D+1⟹6D−2D=1⟹4D=1⟹D=14(Equation 2)
Step 3: Substitute D back into Equation 1 to find A.
From Equation 2, we found D=14. Now substituting this value into Equation 1:
A=3D2=3×142=38
Step 4: Write the nth term using the values of A and D.
Now that we have both A and D:
- A=38
- D=14
We can substitute these values into the formula for the nth term:
Tn=A+(n−1)D=38+(n−1)⋅14
Step 5: Simplify the expression for Tn.
Tn=38+n−14
To combine the terms, we convert 14 to have a common denominator of 8:
14=28
Thus,
Tn=38+2(n−1)8=3+2(n−1)8=3+2n−28=2n+18
Final Answer:
The nth term of the A.P. is:
Tn=2n+18
The nth term of an A.P. is given by the formula:
Tn=A+(n−1)D
where:
- A is the first term,
- D is the common difference,
- n is the term number.
1. The 4th term is equal to 3 times the first term:
T4=3A
Using the formula for the 4th term:
T4=A+3D
Therefore, we have:
A+3D=3A
Rearranging gives us:
3D=3A−A⟹3D=2A⟹A=3D2(Equation 1)
T7=T3+1
Using the formulas for the 7th and 3rd terms:
T7=A+6DandT3=A+2D
Therefore, we have:
A+6D=(A+2D)+1
Simplifying gives:
A+6D=A+2D+1⟹6D−2D=1⟹4D=1⟹D=14(Equation 2)
From Equation 2, we found D=14. Now substituting this value into Equation 1:
A=3D2=3×142=38
Now that we have both A and D:
- A=38
- D=14
Tn=A+(n−1)D=38+(n−1)⋅14
Tn=38+n−14
To combine the terms, we convert 14 to have a common denominator of 8:
14=28
Thus,
Tn=38+2(n−1)8=3+2(n−1)8=3+2n−28=2n+18
The nth term of the A.P. is:
Tn=2n+18
টপার এই প্রশ্নগুলো সমাধান করেছে
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section - B
4 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section -C
7 Videos
- SAMPLE QUESTION PAPERBOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE QUESTION PAPEREXERCISE - Section -C
5 Videos
সম্পর্কিত প্রশ্ন
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
View SolutionA solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right-circular cone mounted on a hemisphere. Find the radius of the hemisphere if the height of the cone is 3 times the radius.
View SolutionA solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right-circular cone mounted on a hemisphere. Find the radius of the hemisphere if the height of the cone is 3 times the radius.
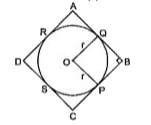
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).
View SolutionThe internal and external radii of a hollow spherical shell are 3 cm and 5 cm-respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder.
View SolutionThe 4 th term of an A.P is equal to the 3 xx ofthe first term and 7 th term exceeds twice the 3 rd term by 1. Find first term and common difference
View SolutionThe 4th term of a G.P. is square of its second term and the first term is -3. Find its 7th term.
View SolutionThe 13th term of an AP is 4 times its 3rd term. If its 5th term is 16 then the sum of its first ten terms is
View SolutionFind the 20^(th) term of an A.P.whose 3^(rd) term is 7 and the 7^(th) term exceeds three times the 3^(rd) term by 2.Also find its n^(th) term (a_(n))
View SolutionIf sum of 3rdand8th terms of an A.P. is 7 and sum of 7thand14th terms is -3 then find 10th term.
View SolutionIf m times the mth term of an A.P. is equal to n times its nth term, then show that the (m + n)th term of the A.P. is zero.
View SolutionIf 6 times of 6th term of an A.P is equal to 7 times the 7th term , then the 13th term of the A.P. is ………… .
View SolutionThe 4th term of a G.P. is square of its second term, and the first term is – 3.Determine its 7th term.
View SolutionIn an A.P. if m times the mth term is equal to n times the nth term then find (m+n)th term.
View SolutionIn an A.P. If m times the mth term is equal to n times the nth term, then find (mn)th term .
View SolutionThe ratio of 7th to 3rd term of an A.P. is 12:5. Find the ratio of 13th to 4th term.
View Solution
