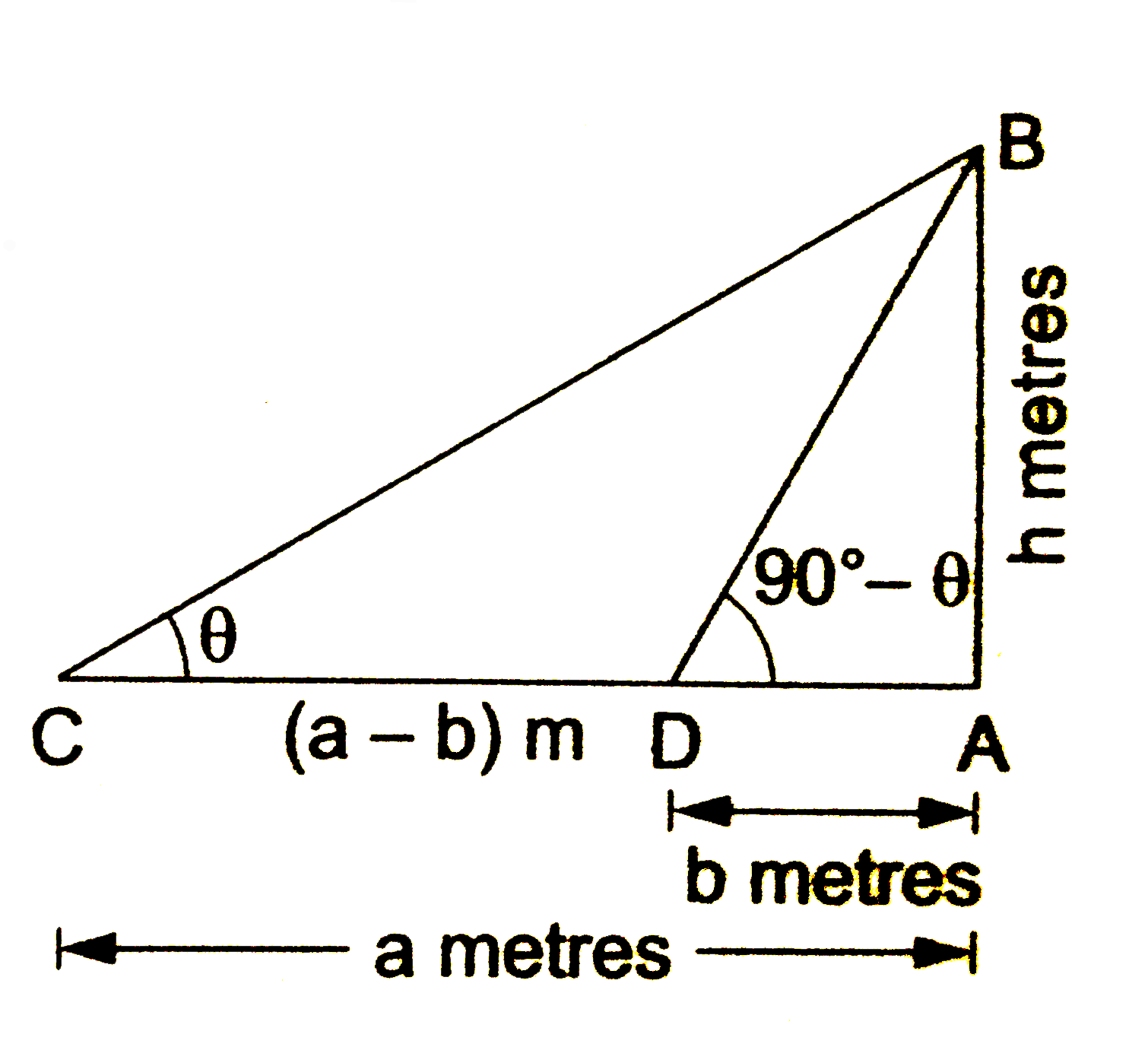
The angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is√ab.
Let AB be the tower and let C and D be the two positions of the observer. Then,
AC= metres and AD=b metres.
Let ∠ACB=θ. Then, ∠ADB=(90∘−θ).
Let AB=h meters.
From right ΔDAB, we have
ABAD=tan(90∘−θ)⇒hb=cotθ
⇒h=btanθ..........(i).
From right ΔCAB, we have
ABAC=tan(90∘−θ)⇒hb=cotθ..........(ii)
From (i) and (ii), we get h2=ab⇒h=√ab.
Hence, the height of the tower is √ab metres.
 .
.
Similar Questions
यदि किसी मीनार के आधार से और एक सरल रेखा में a तथा b दूरी पर स्थित दो बिन्दुओं से मीनार के शीर्ष के उन्नयन कोण पूरक हैं, तो मीनार की ऊँचाई हैं :
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4m and 9m, find the height of the tower from the base of the tower and in the same straight line with it are complementary.
View SolutionThe sum of angles of elevation of the top of a tower from two points distance a and b from the base and in the same straight line with it is 90∘. Then the height of the tower is :
View SolutionThe angle of elevation of the top of a tower of height "h" metres from two points at a distance of "a" and "b" metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab meters.
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is 30∘. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60∘. Find the height of the tower and distance of the tower from the point A.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary.Prove that the height of the tower is 6m.
View Solution