The coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively. The equation of the diagonal CE is:Solution in Bengali
√3x+y=4
x+√3y+4=0
x+√3y=4
none of these
The correct Answer is:C
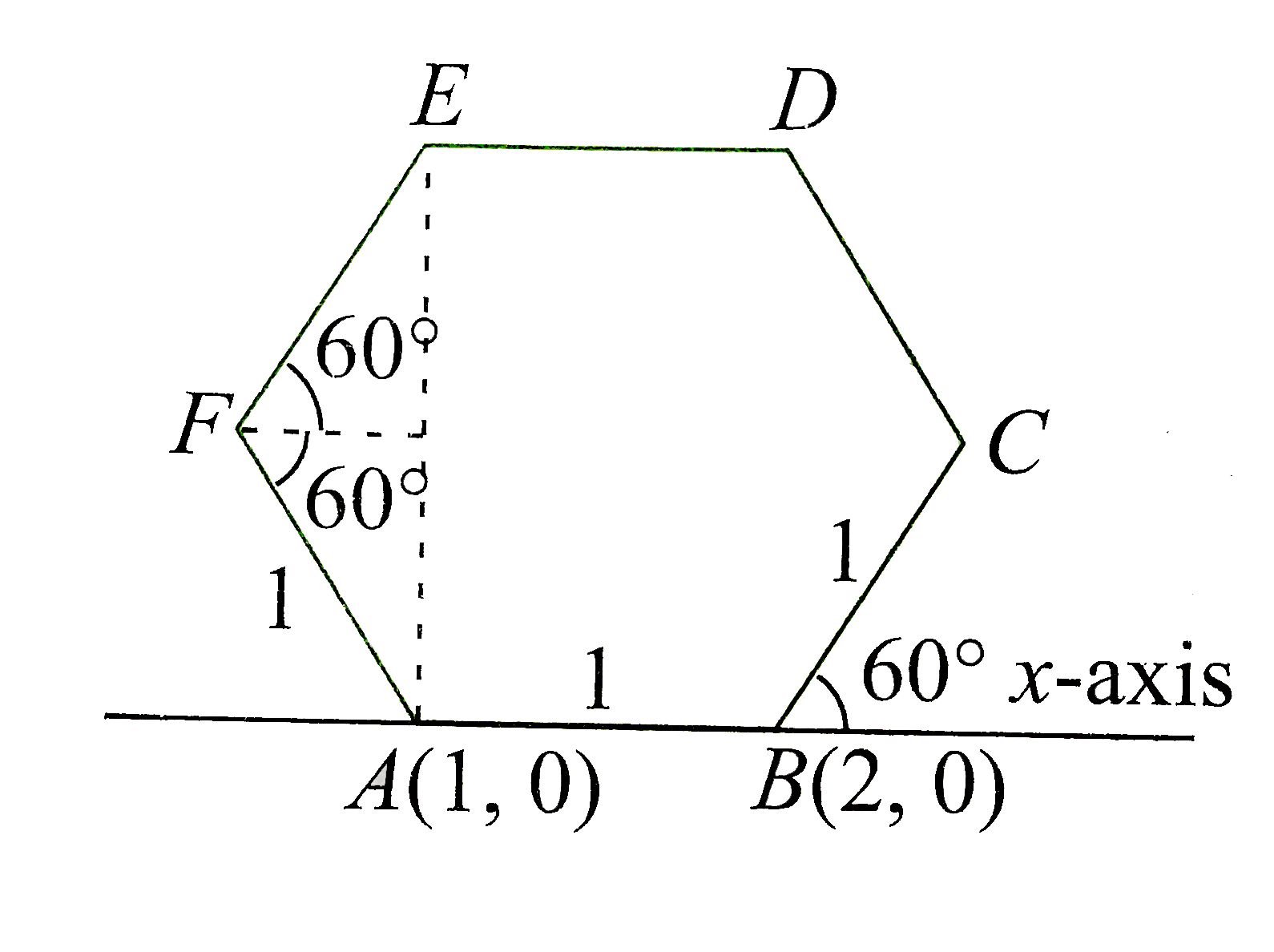
AB=1
or C≡(2+1×cos60∘,1×sin60∘)≡(52,√32)
E≡(1,1×sin60∘+1×sin60∘)≡(1,√3)
Therefore, the equation of CE is
y−√3=−1√3(x−1)
টপার এই প্রশ্নগুলো সমাধান করেছে
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
Explore 29 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:EXERCISE (LINKED COMPREHENSION TYPE)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
সম্পর্কিত প্রশ্ন
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively.The equation of the diagonal CE is:
View SolutionIn a regular hexagon ABCDEF,vec AE
View SolutionIf ABCDEF is a regular hexagon with vec AB=vec a and vec BC=vec b, then vec CE equals
View Solutiona and b form the consecutive sides of a regular hexagon ABCDEF.

View SolutionIf ABCDEF is a regular hexagon with AB = a and BC = b, then CE equals
View SolutionIf ABCDEF is a regular hexagon, then ΔACE is
View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is (a)√3x+y=4 (b) x+√3y+4=0 (c)x+√3y=4 (d) none of these
View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively. The equation of the diagonal CE is:
View SolutionABCDEF is a regular hexagon.
If ¯¯¯¯¯¯AB=¯a,¯¯¯¯¯¯BC=¯b then ¯¯¯¯¯¯CE=
View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is
View Solution
