The height of right circular cylinder of maximum volume in a sphere of diameter 2a is
2√3a
√3a
2a√3
a√3
The correct Answer is:C
Let the radius and height of the cylinder are r and h respectively.
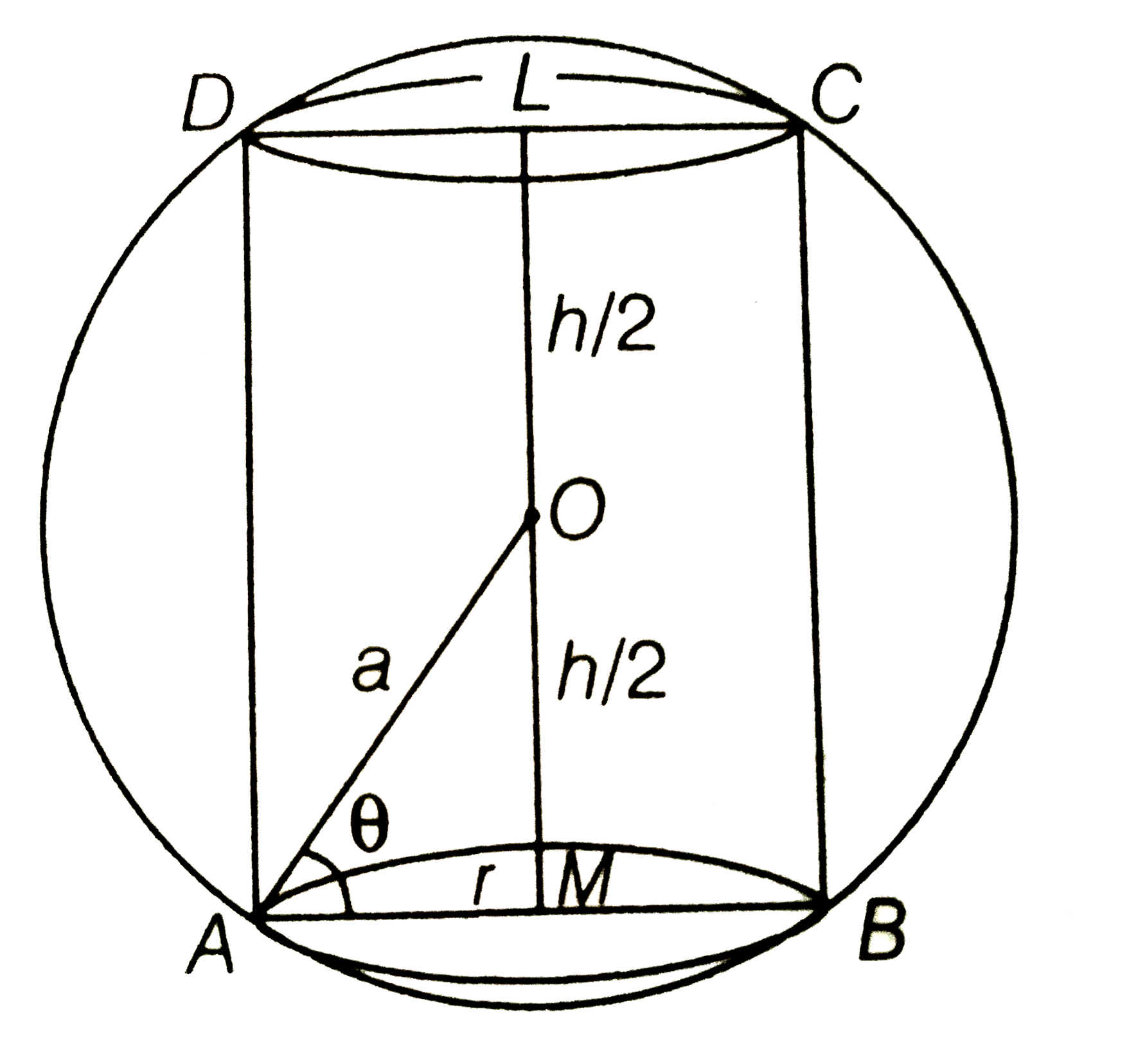
In ΔAOMr2+(h24)=a2⇒r2=a2−h24
Now V=πr2h=π(a2h−14h3)⇒dVdh=π(a2−34h2)
For maximum or minimum
put dVdh=0⇒π(a2−34h2)=0
⇒h=(2√3)a [ ∵h cannot be negative]
Now d2Vdh2=−6h4<0
So, V is maximum at h=2a√3
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MISCELLANEOUS PROBLEMS
Explore 80 Videos
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- BINOMIAL DISTRIBUTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:BINOMIAL DISTRIBUTIONExercise:MHT CET Corner
Explore 6 Videos
Similar Questions
Knowledge Check
The height of a right circular cylinder of maxium volume inscirbed in a sphere of radius 3 is
A√6B2√3C√3D23√3If A denotes the volume of a right circular cylinder of same height as its diameter and B is the volume of a sphere of same radius then AB is :
A43B32C23D34
Prove that the height of a cylinder of maximum volume, inscribed in a sphere of radius 'a' is 2a/√3.
View SolutionShow that the radius of right - circular cylinder of maximum volume, that can be inscribed in a sphere of radius 18 cm, is 6√6cm.
View SolutionThe diameter and height of a right circular cylinder are equal to the diameter of a sphere. Find the ratio of volumes of cylinder and sphere.
View SolutionShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
View SolutionShow that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
View SolutionA right circular cylinder of maximum volume is inscribed in a given right circular cone of height h and base radius r, then radius of cylinder is:
View Solution
