The length of the common chord of the circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2, is
A
2√c2−(a−b)2
B
√4c2−2(a−b)2
C
√2c2−(a−b)2
D
√4c2+2(a−b)2
Video Solution
Text Solution
The correct Answer is:B
The equation of the common chord PQ of the circles
(x−a)2+(y−b)2=c2and(x−b)2+(y−a)2=c2 is
x-y=0 [Using: S1−S2=0]
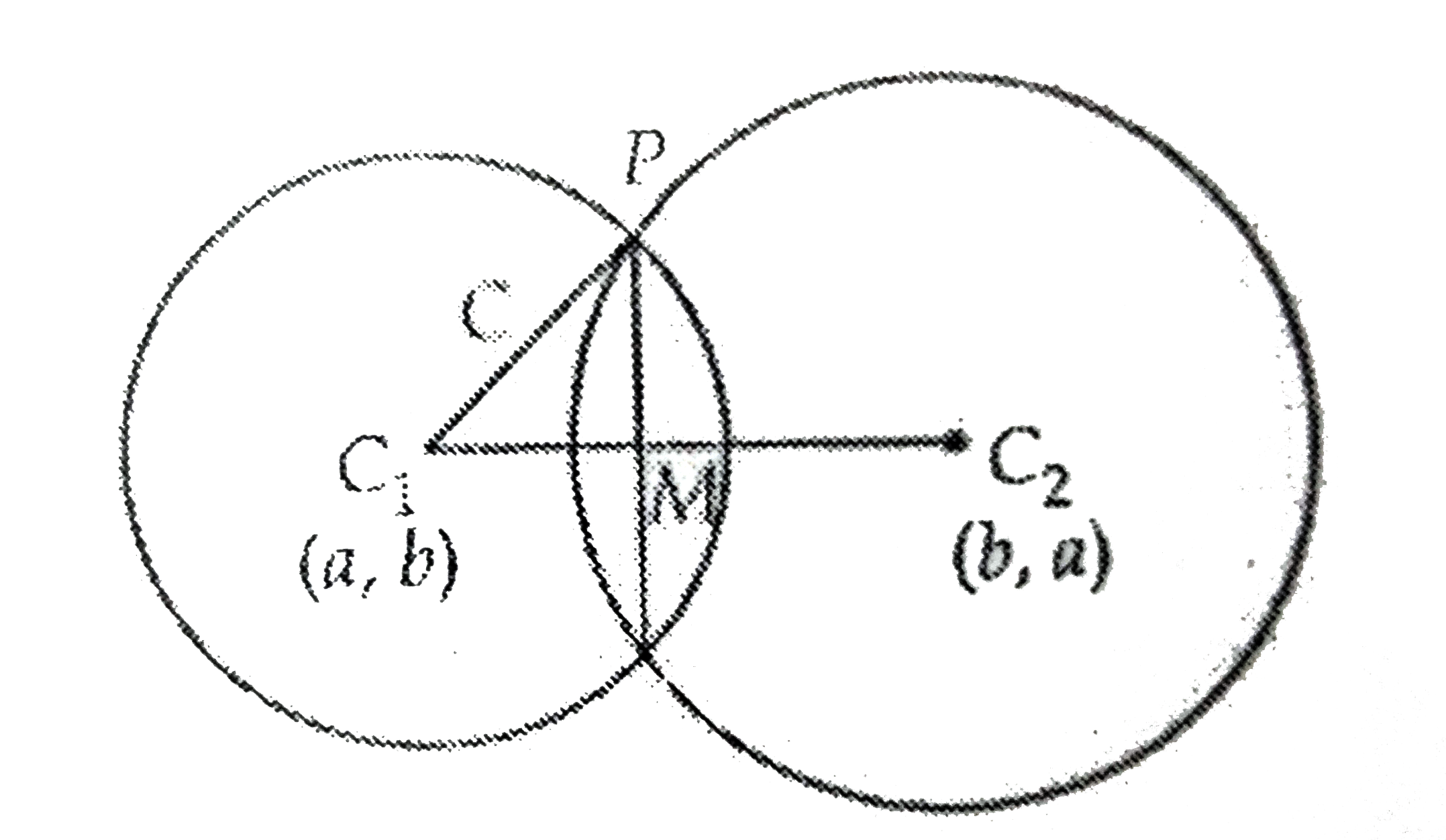
Now,
C1M=Length of perpendicular from (A, b) to x-y=0
⇒C1M=∣∣∣a−b√2∣∣∣
∴PQ=2PM=2√C1P2−C1M2=2√c2−(a−b)22
⇒PQ=2√2c2−(a−b)22=√4c2−2(a−b)2
|
Similar Questions
Knowledge Check
Length of the common chord of the circles
(x−1)2+(y+1)2=c2and(x+1)2+(y−1)2=c2 isA12√c2−2B√c2−2C2√c2−2Dc+2If the circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2 touch each other, then
Aa=b±2cBa=b±√2cCa=b±cDnone of theseIf the circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2 touch each other, then
Aa=b±2cBa=b±√2cCa=b±cDnone of these
The equation of the circle whose diameter is the common chord of the circles (x−a)2+y2=a2 and x2+(y−b)2=b2 is …………
View SolutionThe length of the common chord of the parabolas y2=x and x2=y is
View SolutionThe length of the common chord of the circles x2+y2−2x+4y−20=0,x2+y2+6x+10y−2=0 is
View SolutionThe equation of the circle on the common chord of the circles (x−a)2+y2=a2 and x2+(y+b)2=b2 as diameter, is
View SolutionThe length of the common chord of the circles x2+y2−2x−1=0 and x2+y2+4y−1=0, is
View Solution

