The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The slope of line L can be
(10+5√6)/10
(10−5√6)/10
(8+3√6)/10
none of these
The correct Answer is:B
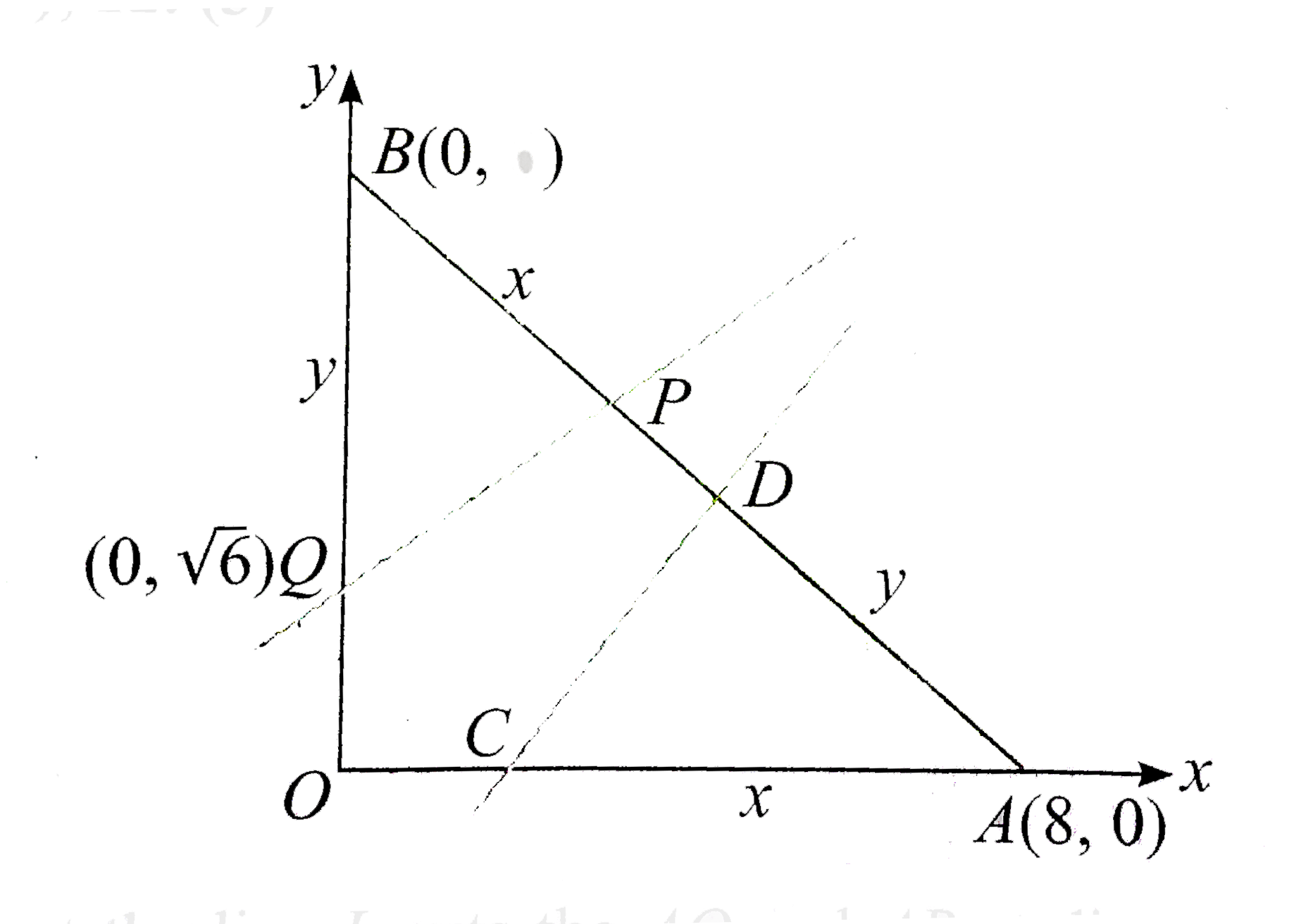
Case I : Let the line L cuts the AO and AB at distances x and y, respectively, from A. Then, the area of the triangle with sides x and y is
12xy sin(∠CAD)=12⋅xy⋅35=3xy10=12
or xy=40
Also, x+y=12 (from perimeter bisection). Then x and y are the roots of r2−12x+40=0 which has imaginary roots.
Case II: if the line L cuts OB and BA at distances y and x, respectively, from B, then we have xy=30 and x+y=12.
Solving, we get x=6+√6 and y=6−√6.
Case III: If the line L cuts the sides OA and OB at distances x and y, respectively, from O, then
x+y=12 and xy=24
∴x,y=6±2√3 (not possible)
So there is a unique line possible. Let point P be (α,β).
Using the parametric equation of AB, we have
β=6−35(6+√6)
and α=45(6+√6)
Hence, the slope of PQ is
β−√6α−0=10−5√610
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Matrix)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Numerical)
Explore 13 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionA straight line l with negative slope passes through (8,2) and cuts the coordinate axes at P and Q. Find absolute minimum value of ''OP+OQ where O is the origin-
View SolutionIf P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionA straight line L is perpendicular to the line 5x−y=1 . The area of the triangle formed by line L, and the coordinate axes is 5. Find the equation of line L.
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The number of such lines possible is
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line L
View SolutionThe line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin , the number of such lines possible is
View SolutionThe line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin .
The slope of the line L can be
View SolutionA straight line L is perpendicular to the line 5x−y=1. The area of the triangle formed by the line L and coordinate axes is 5. The equation of the line L is
View Solutionएक सरल रेखा L, रेखा 5x−y=1 के लम्बवत है। रेखा L तथा निर्देशांक अक्षों से बनने वाले त्रिभुज का क्षेत्रफल 5 है। रेखा L का समीकरण ज्ञात कीजिए।
View SolutionIf area of the triangle formed by the line L perpendicular to 5x−y=1 and the coordinate axes is 5, then the distance of L from the origin is
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The number of such lines possible is a. 1 b. 2 c. 3 d. 4
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line L
View Solution

