The line segment joining points A(2,1) and B(5,-8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x -y + K = 0, find the value of k.
The correct Answer is:-8
To solve the problem, we need to find the value of K such that the point P lies on the line given by the equation 2x−y+K=0. The point P is the trisection point on the line segment joining points A(2,1) and B(5,−8).
Step 1: Find the coordinates of point P using the section formula.
Since P is nearer to A and trisects the line segment AB, we can use the section formula. The ratio of the segments AP and PB is 1:2.
Using the section formula:
P(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)
where m1=1, m2=2, A(2,1) is (x1,y1) and B(5,−8) is (x2,y2).
Step 2: Substitute the values into the section formula.
Px=1⋅5+2⋅21+2=5+43=93=3
Py=1⋅(−8)+2⋅11+2=−8+23=−63=−2
Thus, the coordinates of point P are (3,−2).
Step 3: Substitute the coordinates of point P into the line equation.
Now we substitute P(3,−2) into the line equation 2x−y+K=0:
2(3)−(−2)+K=0
6+2+K=0
8+K=0
Step 4: Solve for K.
K=−8
Conclusion
The value of K is −8.
---
Since P is nearer to A and trisects the line segment AB, we can use the section formula. The ratio of the segments AP and PB is 1:2.
P(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)
where m1=1, m2=2, A(2,1) is (x1,y1) and B(5,−8) is (x2,y2).
Px=1⋅5+2⋅21+2=5+43=93=3
Py=1⋅(−8)+2⋅11+2=−8+23=−63=−2
Thus, the coordinates of point P are (3,−2).
Now we substitute P(3,−2) into the line equation 2x−y+K=0:
2(3)−(−2)+K=0
6+2+K=0
8+K=0
K=−8
The value of K is −8.
Topper's Solved these Questions
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTION)
2 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - BOARD CORNER (VERY SHORT ANSWER TYPE QUESTION)
5 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - BOARD CORNER (Long Solution Type Questions)
6 Videos
- LINES (IN TWO DIMENSIONS) BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO DIMENSIONS) EXERCISE - CASE - BASED MCQs
15 Videos
Similar Questions
If a≠b≠c,prove that(a,a2),(b,b2),(0,0) will not be collinear.
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, 3) and B is (1, 4).
View SolutionProve that sinA−cosA+1sinA+cosA−1=1secA−tanA
View SolutionRead the following text and answer the following questions on the basis of the same :
Class X students of a secondary school in Krishnagar have been allotted a rectangular plot of a land for gardening activity. Saplings of Gulmohar are planted on the boundary at distance of 1 m from each other in the fig. The students are to sow seeds of flowering plants on the remaining area of the plot.
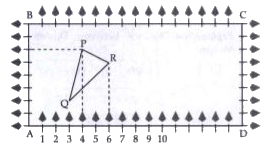
What are the coordinates of A ?
View SolutionThe line segment joining the points P(3,3)andQ(6,−6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x+y+k=0, find the value of k.
View SolutionLet P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
View SolutionPoint P divides the line segment joining the points A(2,1) and B(5,−8) such that APAB=13. If P lies on the line 2x−y+k=0, find the value of k.
View SolutionThe line joining the points (2, 1) and (5, −8) is trisected at the points P and Q . If point P lies on the line 2x−y+k=0 . Find the value of k .
View SolutionPoint P divides the line segment joining the points A(2,1)andB(5,−8) such that APAB=13. If P lies on the line 2x - y + k =0, find the value of k.
View Solutionबिन्दुओं A (2, 1) तथा B (5,-8) को मिलाने वाले रेखाखंड को बिन्दुओं P तथा Q पर समत्रिभाजित किया गया है, जहाँ P, A के पास है। यदि बिन्दु P, रेखा 2x-y+k=0 पर स्थित है, तो k का मान ज्ञात कीजिए।
View SolutionPoint P divides the lne segment joning the points A (2,1) and B(5,−8) such that APAB=13 . If P lies on the line 2x−y+k=0, find the value of k
View Solutionबिंदु P, बिन्दुओ A(2, 1) और B(5, -8) को मिलाने वाले रेखाखण्ड को इस प्रकार विभाजित करता है कि APAB=13 है । यदि P रेखा 2x - y + k = 0 पर स्थित है, तो k का मान ज्ञात कीजिए ।
View SolutionP and Q trisect the line segment joining the points (2,1) and (5,-8) . If the point P lies on 2x-y+k=0, then find the value of k.
View SolutionPoint P divides the line segment joining the points A(2,1) and B(5,−8) such that APAB=13. If P lies on the line 2x−y+k=0, find the value of k.
View SolutionPoint P divides the line segment joining the points A(2,1) and B(5,−8) such that APAB=13. If P lies on the line 2x−y+k=0, find the value of k.
View SolutionThe line segment joining the points P(3,3)andQ(6,−6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x+y+k=0, find the value of k.
View Solution
