The maximum distance of a point on the graph of the function y=√3sinx+cosx from X-axis is
Video Solution
Text Solution
Given that, y=√3sinx+cosx
y=2[√32sinx+12cosx]
=2[sinx⋅cosπ6+cosxsinπ6]
=2sin(x+π/6)
Graph of y = 2sinx
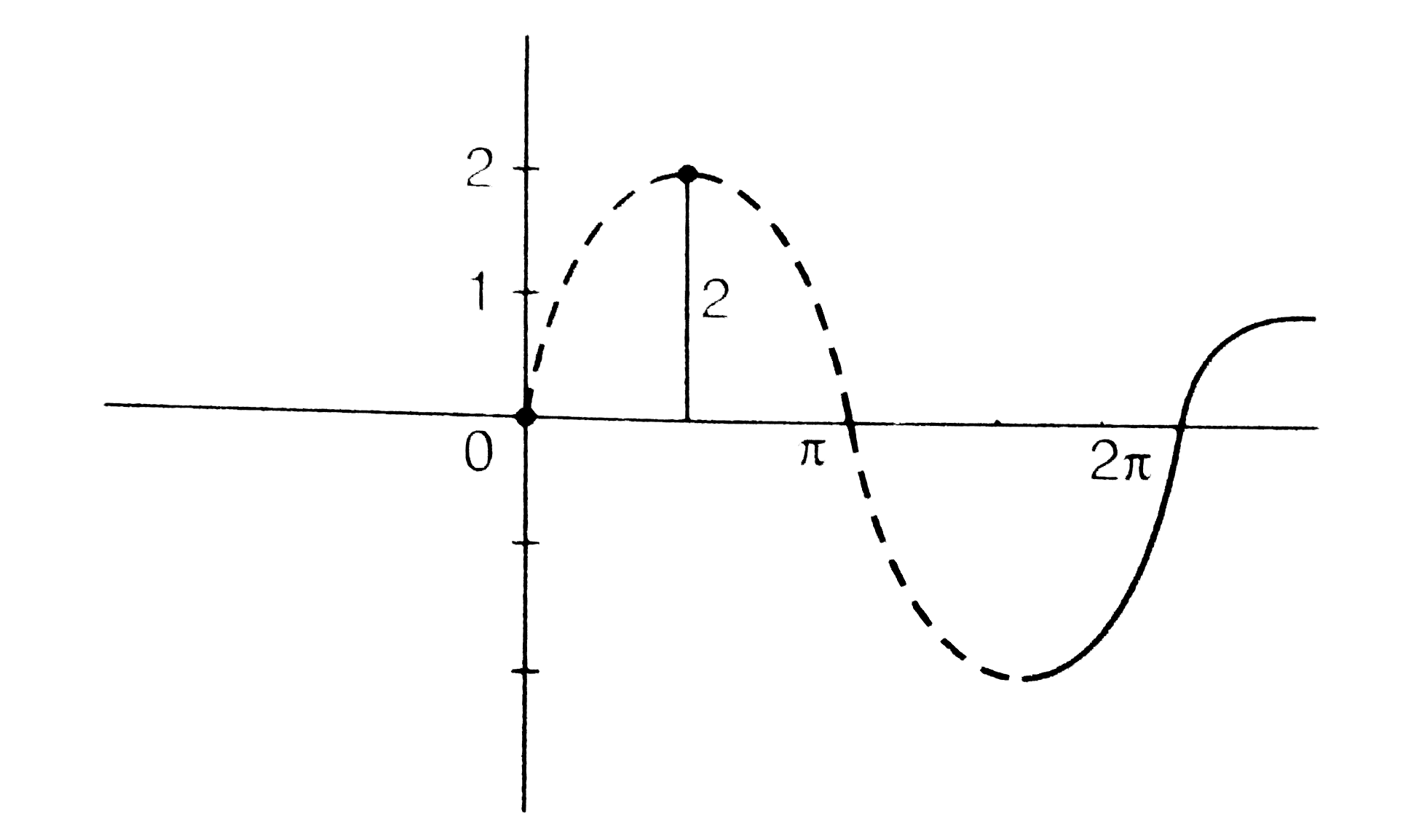
Hence, the maximum distance is 2 units.
|
Similar Questions
Knowledge Check
√3sinx+cosx is maximum when x is
A30∘B90∘C60∘D45∘
Mark the graph of the function
f(x)=|sinx|+|cosx|
View SolutionSketch the graph of the function Y=sinx.
View SolutionIntegrate the functions√tanxsinxcosx
View SolutionFind the maximum value of the function f(x)=sinx+cosx.
View SolutionThe distance of the point (3,5) from the x-axis is
View SolutionThe maximum of the function 3cos x–4sin x is :
View SolutionThe distance of the point (−3,4) from the x-axis is
View Solution
