The median BE and CF of a triangle ABC intersect at G. Prove that the area of ΔGBC= area of the quadrilateral AFGE.
Step by step video solution for The median BE and CF of a triangle ABC intersect at G. Prove that the area of DeltaGBC = area of the quadrilateral AFGE. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Integer/Numerical Value Type )
Explore 5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:Olympiad/HOTS Corner
Explore 14 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Subjective Problems ) (Short Answer Type )
Explore 4 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
Similar Questions
In parallelogram ABCD, AB = 10 cm. The altitudes corresponding to the sides AB and AD are respectively 7 cm and 8 cm. If AD is k cm. Then value of 4 k is
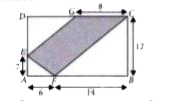
View SolutionIn the given figure ABCD is a rectangle and all measurements are in centimeters. Find the area of the shaded region.
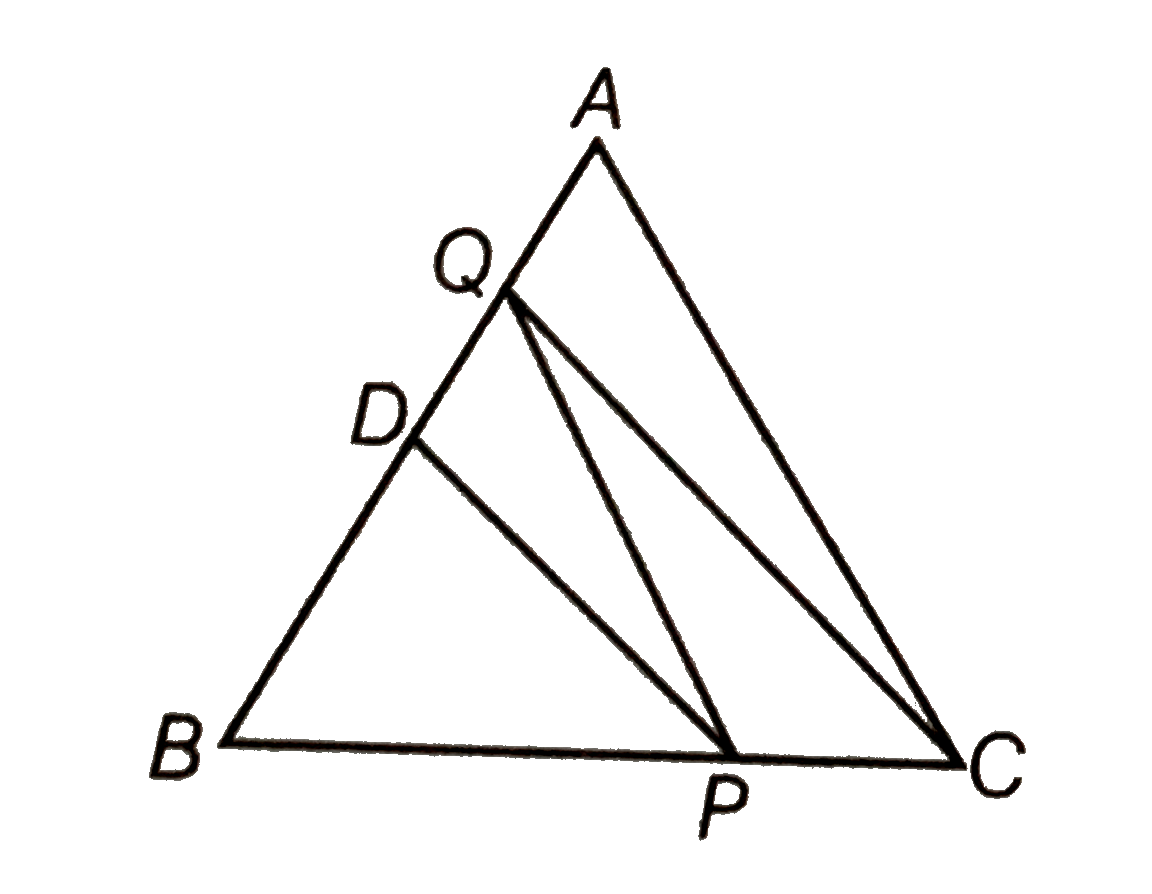
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
View SolutionABCD is a cyclic quadrilateral, if ∠BAC=60∘,∠BCA=20∘, then find the value of ∠ADC.
View SolutionThe medians BE and CF of a triangle ABC intersect at G . Prove that area of GBC=areaofquadrilateralAGFE.
View SolutionIf the median AD and BE of a triangle ABC intersect at 0 ,prove that area of Delta AOB= area of quadrilateral CDOE.
View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of ΔGBC= area of the quadrilateral AFGE.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View Solutionएक त्रिभुज ABC की माध्यिकाऐं BE और CF,G पर प्रतिच्छेद करती हैं दर्शाइए कि ΔGBC का क्षेत्रफल = चतुर्भुज AFGE का क्षेत्रफल
View Solution(ix) AD, BE and CF are the three medians of ΔABC and intersect at G. The area of the ΔABC is 36 Sq. cm. Find (a) the area of ΔAGB and (b) the area of the quadrilateral BDGF.
View SolutionTwo medians BE and CF of ΔABC intersect at G. Prove that area of the quadrilateral AFGE=13ΔABC.
View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of ΔGBC= area of the quadrilateral AFGE.
View SolutionThe median of a triangle ABC intersects BE and CF at point G. Prove that DeltaGBC The area of is equal to the area of the quadrilateral AFGE.
View SolutionΔABC में G केन्द्रक है, तथा AD, BE, व CF त्रिभुज कि मध्यिकाएँ है तो चतुर्भुज BDGF का क्षेत्रफल ज्ञात करे। यदि त्रिभुज ABC का क्षेत्रफल 72 सेमी2है।
View SolutionΔ ABC की तीन माध्यिकाएं AD, BE और CF एक दूसरे को G पर काटती हैं। यदि ABC का क्षेत्रफल 36 वर्ग सेमी हो, तो Δ CGE का क्षेत्रफल है-
View Solution