The number of real solutions (x, y), where |y|=sinx,y=cos−1(cosx),−2π≤x≤2π, is :
2
1
3
4
The correct Answer is:C
Graph of |y| =sin x and y = cos−1 are shown in fig 19 it is evident form the graph that the curves inersect at (0,0)(2,π,0) and (−2π,0) hence there are 3 solution
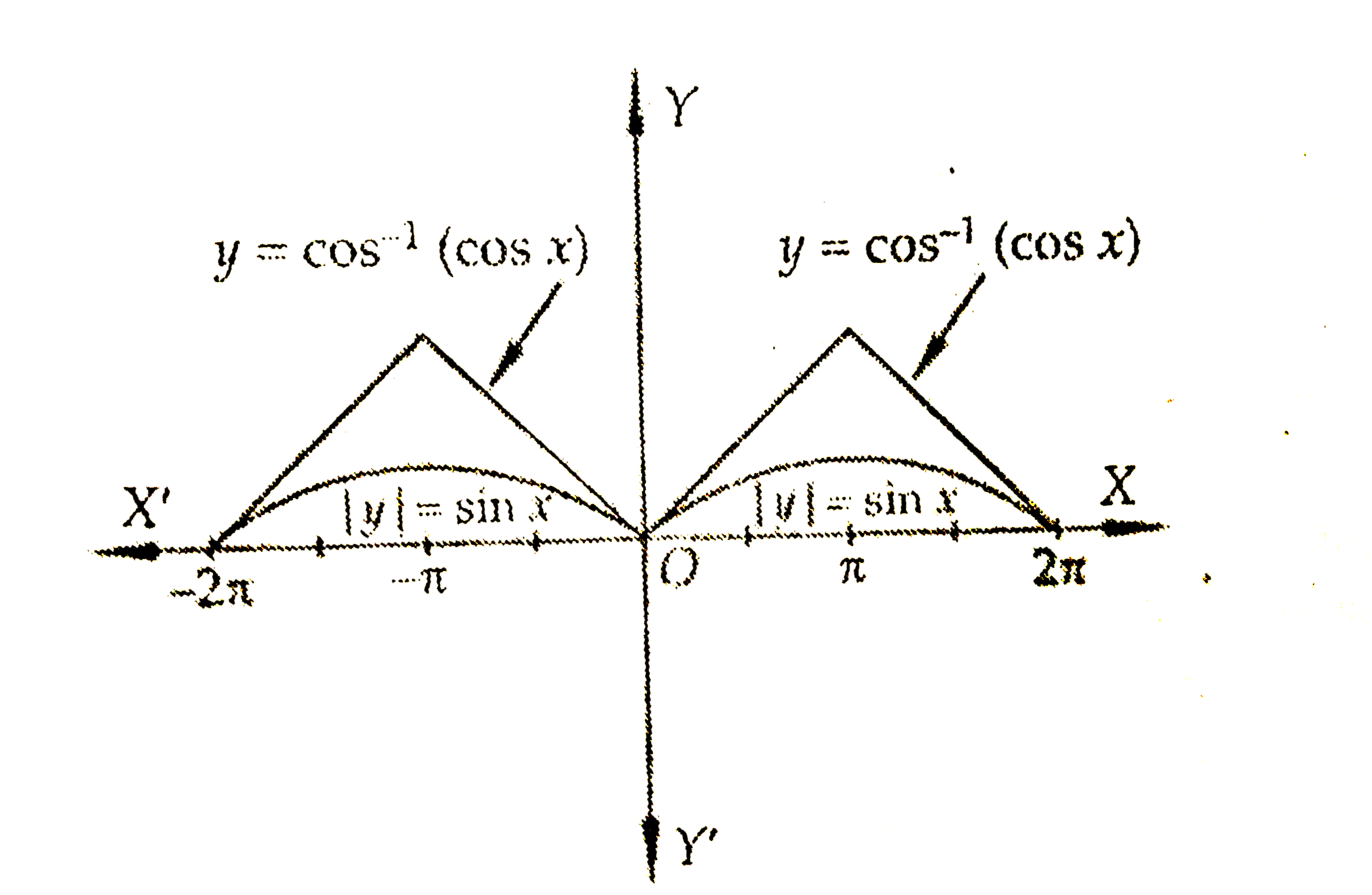
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Section II - Assertion Reason Type
Explore 11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Exercise
Explore 72 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONS Exercise:Chapter Test
Explore 30 Videos
- INDEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:INDEFINITE INTEGRALSExercise:Chapter Test
Explore 30 Videos
- LIMITSBook:OBJECTIVE RD SHARMA ENGLISHChapter:LIMITSExercise:Chapter Test
Explore 58 Videos
Similar Questions
Statement -1: If x<√ethen
cot−1{log(e/x2)log(ex2)}+cot−1{log(ex4)log(e2/x2))}=π−tan−13
statement 2:tan−1(x+y)1−xy=tan−1x+tan−1yifxy<1
View SolutionIf θ∈[4π,5π]thencos−1(cosθ) equals
View SolutionSolve sin−1(1−x)−2sin−1x=π2
View SolutionThe integral ∫2x−3(x2+x+1)2.dx is equal to
View SolutionLet f(x)=⎧⎪⎨⎪⎩x2xεZd(x2−4)2−xx∉Z the set of integers. Then limx→2f(x)
View SolutionDraw the graph of the functions on the same axes: y=sinx and y=cosx,0≤x≤2π
View SolutionThe area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is
View SolutionThe equation sinx+siny+sinz=−3 for 0≤x≤2π, 0≤y≤2π,o≤z≤2π, has
View SolutionIf 0≤x≤2πand|cosx|≤sinx, the
View SolutionThe equation of tangents to the curve y=cos(x+y),−2π≤x≤2π that are parallel to the line x+2y=0, is
View Solutionthe equation sin x + sin y + sin z = - 3 for 0 le x le 2pi , 0 le y le 2pi , 0 le z le 2pi Of
View SolutionThe area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is
View SolutionIf 0 le x le 2pi Then the equation sin^(8) x + cos ^(6) x=1 K is the number of solutions.
View SolutionFind the equation of tangents to the curve y=cos(x+y),−2π≤x≤2π that are parallel to the line x+2y=0
View SolutionThe number of real solutions of |y|=sinx,y=cos−1(cosx),−2π≤x≤2π is
View SolutionThe equation sinx+siny+sinz=−3 for 0≤x≤2π, 0≤y≤2π,o≤z≤2π, has
View Solution
