The perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
The correct Answer is:9.6cm
To solve the problem of finding the corresponding side of the second triangle, we can follow these steps:
Step 1: Understand the relationship between the triangles
Since the two triangles are similar, the ratio of their corresponding sides is equal to the ratio of their perimeters.
Step 2: Write down the given information
- Perimeter of the first triangle (Triangle ABC) = 30 cm
- Perimeter of the second triangle (Triangle DEF) = 24 cm
- One side of the first triangle (AB) = 12 cm
- We need to find the corresponding side of the second triangle (DE).
Step 3: Set up the ratio of the perimeters
The ratio of the perimeters of the two triangles can be expressed as:
Perimeter of Triangle ABCPerimeter of Triangle DEF=3024
Step 4: Simplify the ratio
To simplify the ratio:
3024=54
This means that the ratio of any corresponding sides of the triangles is also 54.
Step 5: Set up the equation for the corresponding sides
Using the ratio of the sides, we can write:
ABDE=54
Substituting the known value of AB:
12DE=54
Step 6: Cross-multiply to solve for DE
Cross-multiplying gives:
12⋅4=5⋅DE
48=5⋅DE
Step 7: Solve for DE
Now, divide both sides by 5 to find DE:
DE=485=9.6 cm
Conclusion
The corresponding side of the second triangle (DE) is 9.6 cm.
---
Since the two triangles are similar, the ratio of their corresponding sides is equal to the ratio of their perimeters.
- Perimeter of the first triangle (Triangle ABC) = 30 cm
- Perimeter of the second triangle (Triangle DEF) = 24 cm
- One side of the first triangle (AB) = 12 cm
- We need to find the corresponding side of the second triangle (DE).
The ratio of the perimeters of the two triangles can be expressed as:
Perimeter of Triangle ABCPerimeter of Triangle DEF=3024
To simplify the ratio:
3024=54
This means that the ratio of any corresponding sides of the triangles is also 54.
Using the ratio of the sides, we can write:
ABDE=54
Substituting the known value of AB:
12DE=54
Cross-multiplying gives:
12⋅4=5⋅DE
48=5⋅DE
Now, divide both sides by 5 to find DE:
DE=485=9.6 cm
The corresponding side of the second triangle (DE) is 9.6 cm.
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(D)
Explore 18 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(E)
Explore 61 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Book:ICSEChapter:SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)Exercise:EXERCISE 15(B)
Explore 17 Videos
- SIMILARITY Book:ICSEChapter:SIMILARITY Exercise:MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
Explore 10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Book:ICSEChapter:SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)Exercise:Exercise 6(e )
Explore 18 Videos
Similar Questions
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B'C' Calculate :
the length of AB, if A' B' = 6 cm.
View SolutionIn the following figure, XY is parallel to BC,AX=9cm,XB=4.5cmandBC=18cm.
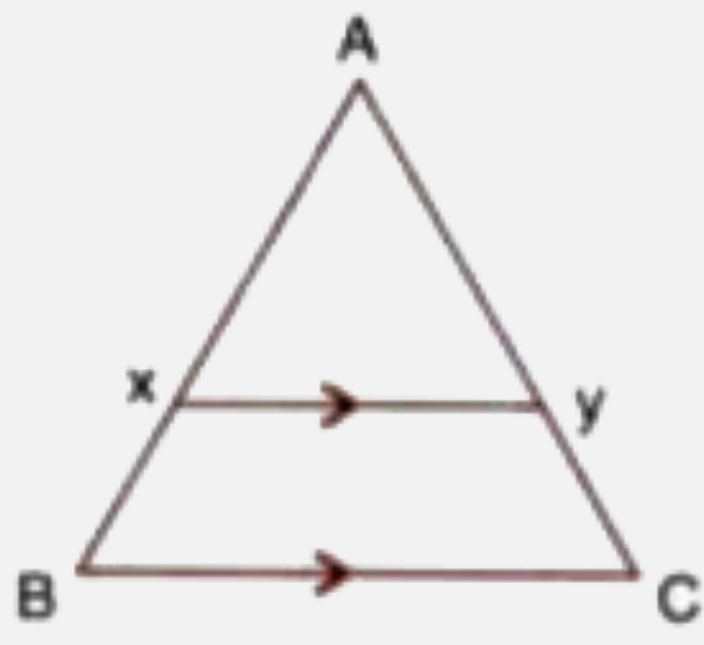
AYYC
View SolutionIn the following figure, point D divides AB in the ratio 3: 5. Find :
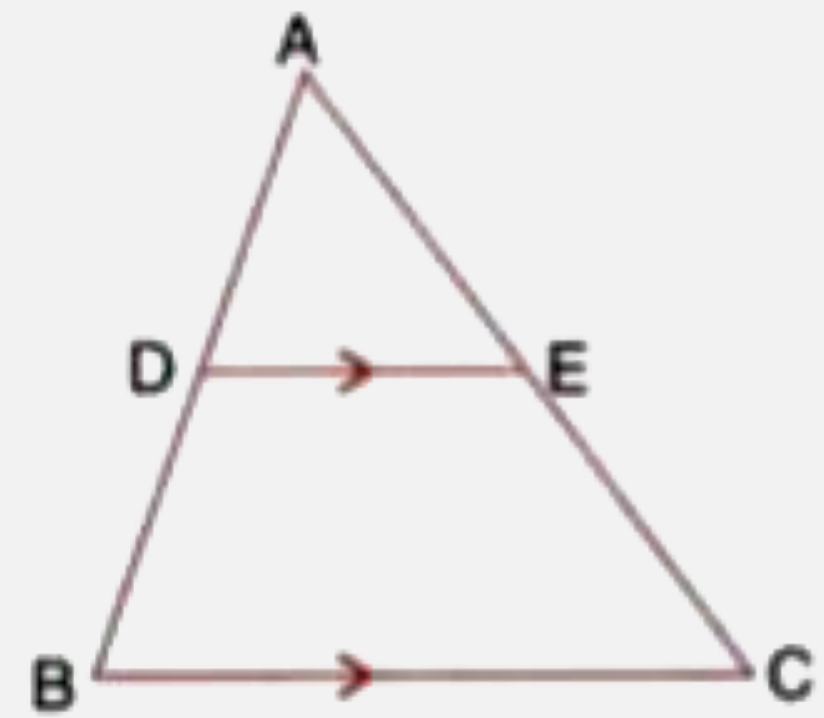
AEEC
View SolutionA girl, named Ritika of height 90 cm is walking away from the ase of a lamp-post, She observes the shadows of lamp-post and herself and relate it with a chapter of mathematics, she studied in her last class.
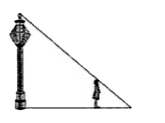
On the basis of information, answer the following question
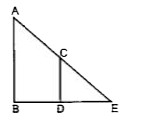
The triangles ABE and CDE are similar by which of the following similarity rule ?
View SolutionThe distance between two towns A and B is 216 km, and by rail it is 208 km. A car travels at a speed of xkm/hr and the train travels at a speed which is 16km/hr faster than the car. Calculate :
(i) the time taken by the car to reach town B from A, in terms of x,
(i) the time taken by ht etrain, to reach town B from A, in terms of .
(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x, and solve it.
(iv) Hence, find the speed of the train.
View Solutionthe perimeters of two similar triangles are 40 cm and 30 cm respectively. If one side of the first traingle is 21 cm. Determine the corresponding side of the second triangle.
View Solutionदो समरूप त्रिभुजों के परिणाम (Perimeters ) क्रमशः 30 सेमी और 20 सेमी हैं । यदि पहले त्रिभुज की एक भुजा की लम्बाई 12 सेमी हो , तो दूसरे त्रिभुज की संगत भुजा की लम्बाई कीजिए ।
View Solutionदो समरूप त्रिभुजों का परिमाप क्रमशः 25 सेमी० तथा 15 सेमी० है | यदि पहले त्रिभुज की एक भुजा 9 सेमी० है तो उसके संगत दूसरे त्रिभुज की भुजा ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों के परिमाप क्रमशः 25 सेमी और 15 सेमी है यदि पहले त्रिभुज की एक भुजा 9 सेमी है तो दूसरे त्रिभुज की संगत भुजा ज्ञात कीजिये
View Solutionदो समरूप त्रिभुजों के परिमाप 30 सेमी और 20 सेमी है यदि पहले त्रिभुज की एक भुजा 12 सेमी है तो दूसरे त्रिभुज की संगत भुजा ज्ञात कीजिये
View SolutionThe perimeters of two similar triangle are 30 cm and 20 cm respectively. IF one side of the first Triangle is 12 cm. determine the corresponding side of the second Triangle.
View SolutionThe perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
View SolutionThe perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
View SolutionThe perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
View SolutionThe perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
View Solution