The production of TV in a factory increases uniformly by a fixed number every year .It produced 8000 TV's in 6th year & 11300 in 9th year , find the production in 8th year .
10500
9800
9700
10200
The correct Answer is:10200
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Problem
The production of TVs in a factory increases uniformly by a fixed number every year, forming an arithmetic progression (AP). We know the production in the 6th year and the 9th year.
Step 2: Define the Variables
Let:
- A be the first term (the production in the first year).
- d be the common difference (the fixed increase in production each year).
- An be the production in the nth year.
From the problem:
- A6=8000 (production in the 6th year)
- A9=11300 (production in the 9th year)
Step 3: Write the Equations
Using the formula for the nth term of an AP:
An=A+(n−1)d
We can write:
1. For the 6th year:
A6=A+(6−1)d=A+5d=8000(Equation 1)
2. For the 9th year:
A9=A+(9−1)d=A+8d=11300(Equation 2)
Step 4: Subtract the Equations
Now, we can subtract Equation 1 from Equation 2 to eliminate A:
(A+8d)−(A+5d)=11300−8000
This simplifies to:
3d=3300
Step 5: Solve for d
Now, divide both sides by 3:
d=33003=1100
Step 6: Substitute d Back to Find A
Now, substitute d back into Equation 1 to find A:
A+5(1100)=8000
This simplifies to:
A+5500=8000
Subtract 5500 from both sides:
A=8000−5500=2500
Step 7: Find the Production in the 8th Year
Now we can find the production in the 8th year using the formula:
A8=A+(8−1)d=A+7d
Substituting the values of A and d:
A8=2500+7(1100)=2500+7700=10200
Final Answer
The production in the 8th year is 10,200 TVs.
---
The production of TVs in a factory increases uniformly by a fixed number every year, forming an arithmetic progression (AP). We know the production in the 6th year and the 9th year.
Let:
- A be the first term (the production in the first year).
- d be the common difference (the fixed increase in production each year).
- An be the production in the nth year.
- A6=8000 (production in the 6th year)
- A9=11300 (production in the 9th year)
Using the formula for the nth term of an AP:
An=A+(n−1)d
We can write:
1. For the 6th year:
A6=A+(6−1)d=A+5d=8000(Equation 1)
2. For the 9th year:
A9=A+(9−1)d=A+8d=11300(Equation 2)
Now, we can subtract Equation 1 from Equation 2 to eliminate A:
(A+8d)−(A+5d)=11300−8000
This simplifies to:
3d=3300
Now, divide both sides by 3:
d=33003=1100
Now, substitute d back into Equation 1 to find A:
A+5(1100)=8000
This simplifies to:
A+5500=8000
Subtract 5500 from both sides:
A=8000−5500=2500
Now we can find the production in the 8th year using the formula:
A8=A+(8−1)d=A+7d
Substituting the values of A and d:
A8=2500+7(1100)=2500+7700=10200
The production in the 8th year is 10,200 TVs.
Topper's Solved these Questions
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - EXERCISE (MATCH THE FOLLOWING )
2 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - EXERCISE (ASSERTION & REASON TYPE )
5 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - EXERCISE (MULTIPLE CHOICE QUESTION )(LEVEL 1 )
35 Videos
- AREAS RELATED TO CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - OLYMPIAD/HOTS CORNER
30 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Olympiad/HOTS Corner
30 Videos
Similar Questions
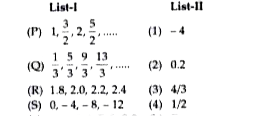
Match the A.P. given in List - I with their common difference given in List - II
View SolutionThe nth term of a sequence is 3n−2 is the sequence an A.P.? If so, find its 10th term.
View SolutionFind the sum to 200 terms of the series 1+4+6+5+11+6+….
View SolutionAn equilateral triangle is inscribed in a circle of circumference equal to perimeter of a square with side 22 cm. Find its side.
View SolutionIn the given figure (not drawn to scale), BD is a diameter of the circle with centre O. C and A are two points on the circle. BA and CD, when produced, meet at E. If ∠DOC=60∘and∠ABD=23∘, then find ∠OBC.

View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find :(i) the production in the 1st year(ii) the production in the 10th year(iii) the total production in first 7 years
View SolutionA manufacturer of radio sets produced 600 units in the third year and 700 units in the seventh year. Assuming that the product increases uniformly by a fixed number every year, find i. the production in the first year ii. the total product in 7 years and iii. the product in the 10th year.
View SolutionA manufacturre of TV sets produced 6000 units in the third year and 7000 units in the seventh year. Assuming that the production increases uniformaly by fixed number every year, find the production increases uniformly, by a fixed number every year, find the production (i) in the first year, (ii) in the 10th year, (iii) in 7 years.
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increase unifformaly by a fixed number evergy year, find :
(ii) the production in the 10th year.
View SolutionA manufacture of TV sets produced 500 sets in the third year and 700 sets in the seventh year. Assuming that the production increase uniformly by a fixed number every year. Find.
(i) The production of TV sets in the 15th year.
View SolutionA manufacturer of wire produced 1400 m wire in the 5 th year and 1600 m in the 9th year. Assuming that the production increases uniformly by a fixed number every year, find
(i) the production in the 12th year.
(ii) in which year the production will be 1900 m?
(iii) the total production in 9 years.
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by fixed number every year , find
the production in the 1st year
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by fixed number every year , find
the production in the 10th year
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets I the seventh year. Assuming that the production increases uniformly by a fixed number every year, find : the production in the 1st year
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets I the seventh year. Assuming that the production increases uniformly by a fixed number every year, find : the production in the 10th year
View Solution
