The space s described in time t by a particle moving in a straight line is given by s=t5−40t3+30t2+80t−250 . Find the minimum value of acceleration.
To find the minimum value of acceleration for the particle moving in a straight line, we will follow these steps:
Step 1: Find the expression for acceleration
The space s described by the particle is given by:
s=t5−40t3+30t2+80t−250
To find acceleration, we first need to find the first derivative of s with respect to time t, which gives us the velocity v:
v=dsdt=ddt(t5−40t3+30t2+80t−250)
Calculating the derivative:
v=5t4−120t2+60t+80
Next, we find the second derivative of s with respect to t, which gives us the acceleration a:
a=d2sdt2=ddt(5t4−120t2+60t+80)
Calculating the second derivative:
a=20t3−240t+60
Step 2: Find the critical points of acceleration
To find the minimum value of acceleration, we need to find the critical points by setting the first derivative of acceleration to zero:
dadt=60t2−240=0
Solving for t:
60t2=240⟹t2=4⟹t=2 or t=−2
Step 3: Determine the nature of the critical points
To determine whether these critical points are minima or maxima, we take the second derivative of acceleration:
d2adt2=120t
Now we evaluate this at the critical points t=2 and t=−2:
- For t=2:
d2adt2=120×2=240>0(indicates a minimum)
- For t=−2:
d2adt2=120×(−2)=−240<0(indicates a maximum)
Step 4: Calculate the minimum value of acceleration
Now we substitute t=2 back into the acceleration equation to find the minimum value:
a=20(23)−240(2)+60
Calculating this:
a=20(8)−480+60=160−480+60=220−480=−260
Thus, the minimum value of acceleration is:
−260
The space s described by the particle is given by:
s=t5−40t3+30t2+80t−250
To find acceleration, we first need to find the first derivative of s with respect to time t, which gives us the velocity v:
v=dsdt=ddt(t5−40t3+30t2+80t−250)
Calculating the derivative:
v=5t4−120t2+60t+80
a=d2sdt2=ddt(5t4−120t2+60t+80)
Calculating the second derivative:
a=20t3−240t+60
To find the minimum value of acceleration, we need to find the critical points by setting the first derivative of acceleration to zero:
dadt=60t2−240=0
Solving for t:
60t2=240⟹t2=4⟹t=2 or t=−2
To determine whether these critical points are minima or maxima, we take the second derivative of acceleration:
d2adt2=120t
Now we evaluate this at the critical points t=2 and t=−2:
- For t=2:
d2adt2=120×2=240>0(indicates a minimum)
- For t=−2:
d2adt2=120×(−2)=−240<0(indicates a maximum)
Now we substitute t=2 back into the acceleration equation to find the minimum value:
a=20(23)−240(2)+60
Calculating this:
a=20(8)−480+60=160−480+60=220−480=−260
−260
Topper's Solved these Questions
Similar Questions
Velocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
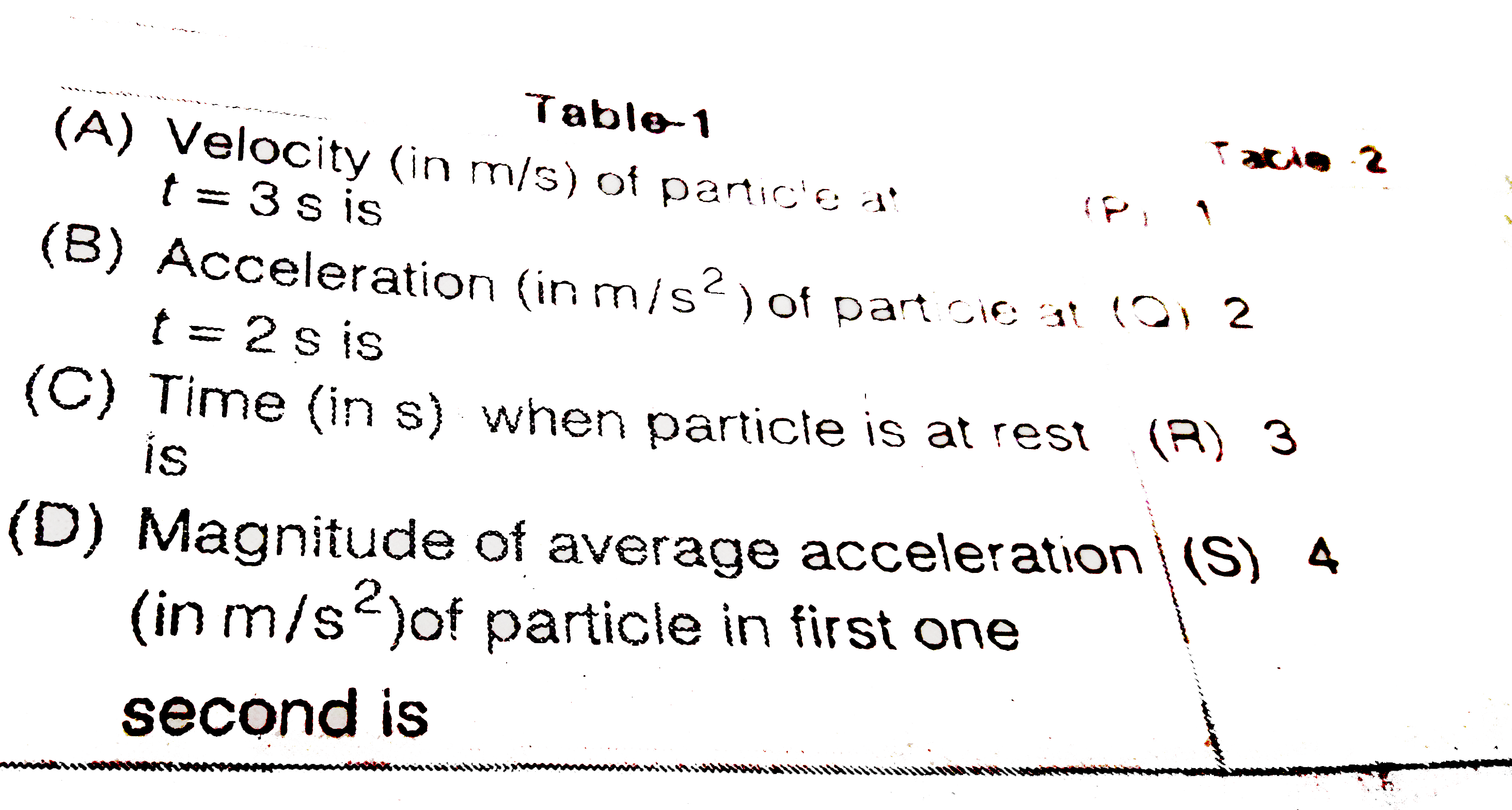
View SolutionAt time t , the displacement of a particle moving in a straight line by x=−4t2+2t . Find the velocity and acceleration a when t = (1/2) s .
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+c. Then prove that acceleration is proportional to s−3.
View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+⋅ Then prove that acceleration is proportional to s−3.
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum and acceleration minimum.
View SolutionA particle moves along a staight line such that its displacement at any time t is given by s=t3−6t2+3t+4m. Find the velocity when the acceleration is 0.
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution

