The two vertices of a triangle are (7,13)and(−4,2) and it's centroid is (3,1) , then the third vertex is
To find the third vertex of the triangle given two vertices and the centroid, we can follow these steps:
Step 1: Understand the Centroid Formula
The coordinates of the centroid G(x,y) of a triangle with vertices A(x1,y1), B(x2,y2), and C(x3,y3) are given by:
G=(x1+x2+x33,y1+y2+y33)
Step 2: Assign Known Values
We know:
- Vertex A: A(7,13) → x1=7,y1=13
- Vertex B: B(−4,2) → x2=−4,y2=2
- Centroid G: G(3,1) → Gx=3,Gy=1
Step 3: Set Up the Equations
Using the centroid formula, we can set up the following equations:
1. For the x-coordinates:
3=7+(−4)+x33
2. For the y-coordinates:
1=13+2+y33
Step 4: Solve for x3
Multiply both sides of the first equation by 3:
9=7−4+x3
Simplify:
9=3+x3
Subtract 3 from both sides:
x3=6
Step 5: Solve for y3
Multiply both sides of the second equation by 3:
3=13+2+y3
Simplify:
3=15+y3
Subtract 15 from both sides:
y3=−12
Step 6: State the Third Vertex
Thus, the coordinates of the third vertex C are:
C(6,−12)
Final Answer
The third vertex of the triangle is (6,−12).
---
The coordinates of the centroid G(x,y) of a triangle with vertices A(x1,y1), B(x2,y2), and C(x3,y3) are given by:
G=(x1+x2+x33,y1+y2+y33)
We know:
- Vertex A: A(7,13) → x1=7,y1=13
- Vertex B: B(−4,2) → x2=−4,y2=2
- Centroid G: G(3,1) → Gx=3,Gy=1
Using the centroid formula, we can set up the following equations:
1. For the x-coordinates:
3=7+(−4)+x33
2. For the y-coordinates:
1=13+2+y33
Multiply both sides of the first equation by 3:
9=7−4+x3
Simplify:
9=3+x3
Subtract 3 from both sides:
x3=6
Multiply both sides of the second equation by 3:
3=13+2+y3
Simplify:
3=15+y3
Subtract 15 from both sides:
y3=−12
Thus, the coordinates of the third vertex C are:
C(6,−12)
The third vertex of the triangle is (6,−12).
Topper's Solved these Questions
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Triangles) (Very Short Answer type Questions )
Explore 17 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Triangles) (Long Answer Type Questions)
Explore 4 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
Explore 11 Videos
- COORDINATE GEOMETRYBook:OSWAL PUBLICATIONChapter:COORDINATE GEOMETRYExercise:SELF ASSESSMENT
Explore 20 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
Similar Questions
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
View SolutionShow that the points (−2,5),(3,−4)and(7,10) are the vertices of the right angled triangle .
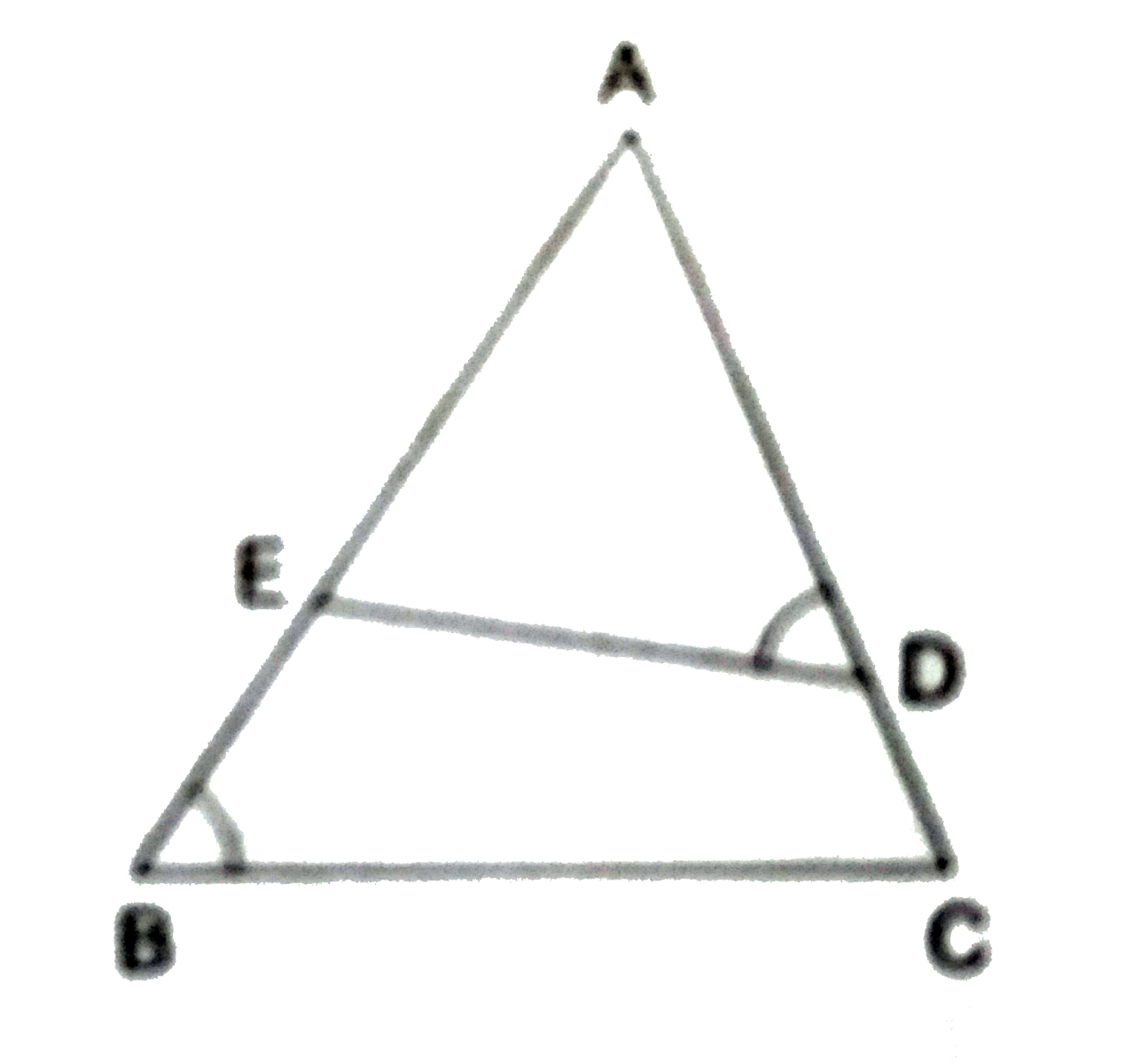
View SolutionIn the given figure, if ∠ADE=∠B, show that ΔADE~ΔABC. If AD=3.8cm,AE=3.6cm,BE=2.1cm,andBC=4.2cm, find DE.
View SolutionFind the point on the X -axis which is equidistant from the points A(2,−5)andB(−2,9)
View SolutionIn ΔABC right - angled at c, AB = 29 units BC = 21 units and ∠ABC=θ Determine the value of
cos2θ+sin2θand
View SolutionThe coordinates of the centroid of a triangle are (1,3) and two of its vertices are (-7,6) and (8,5). Find the third vertex.Also find the coordinates of the centroid of the triangle when the third vertex is (2,4) .
View SolutionFind the third vertex of a triangle,if two of its vertices are at (-3,1) and (0,-2) and the centroid is at the origin.
View SolutionFind the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
View SolutionThe two vertices of a triangle are (-4,3) and (2,6) If the centroid is at origin then the third vertex is
View SolutionIf the centroid of a triangle is at (10,-1) and two vertices are (3,2) and (5,-11). Find the third vertex of a triangle .
View SolutionIf the centroid of a triangle is at (4,-2) and two of its vertices are (3,-2) an (5,2) then find the third vertex of the triangle .
View SolutionTwo vertices of a triangle are (3,1) (-6,5) and the centroid is at the origin. Find the third vertex of the triangle.
View SolutionTwo vertices of a triangle are at the points (5,−2),(−3,6) and the centroid is at the (3,1).Then the coordinates of the remaining vertex
View SolutionTwo vertices of a △ABC are B (- 3,1) and C (0,-2) and its centroid is at the origin. The third vertex A is:
View SolutionFind the third vertex of a triangle , if two of its vertices are at (-3,1) and (0,-2) and the centroid is at the origin.
View Solutionत्रिभुज के दो शीर्षों तथा केन्द्रक के निर्देशांक क्रमशः (3,4),(-1,-9) तथा (2,-4) हैं, तो त्रिभुज के तीसरे शीर्ष के निर्देशांक हैं
View Solution