Through a fixed point (h,k), secant are drawn to the circle x2+y2=r2. Show that the locus of the midpoints of the secants by the circle is x2+y2=hx+ky.
From the diagram,
CM⊥BP
∴(y1x1)(y1−kx1−h)=−1
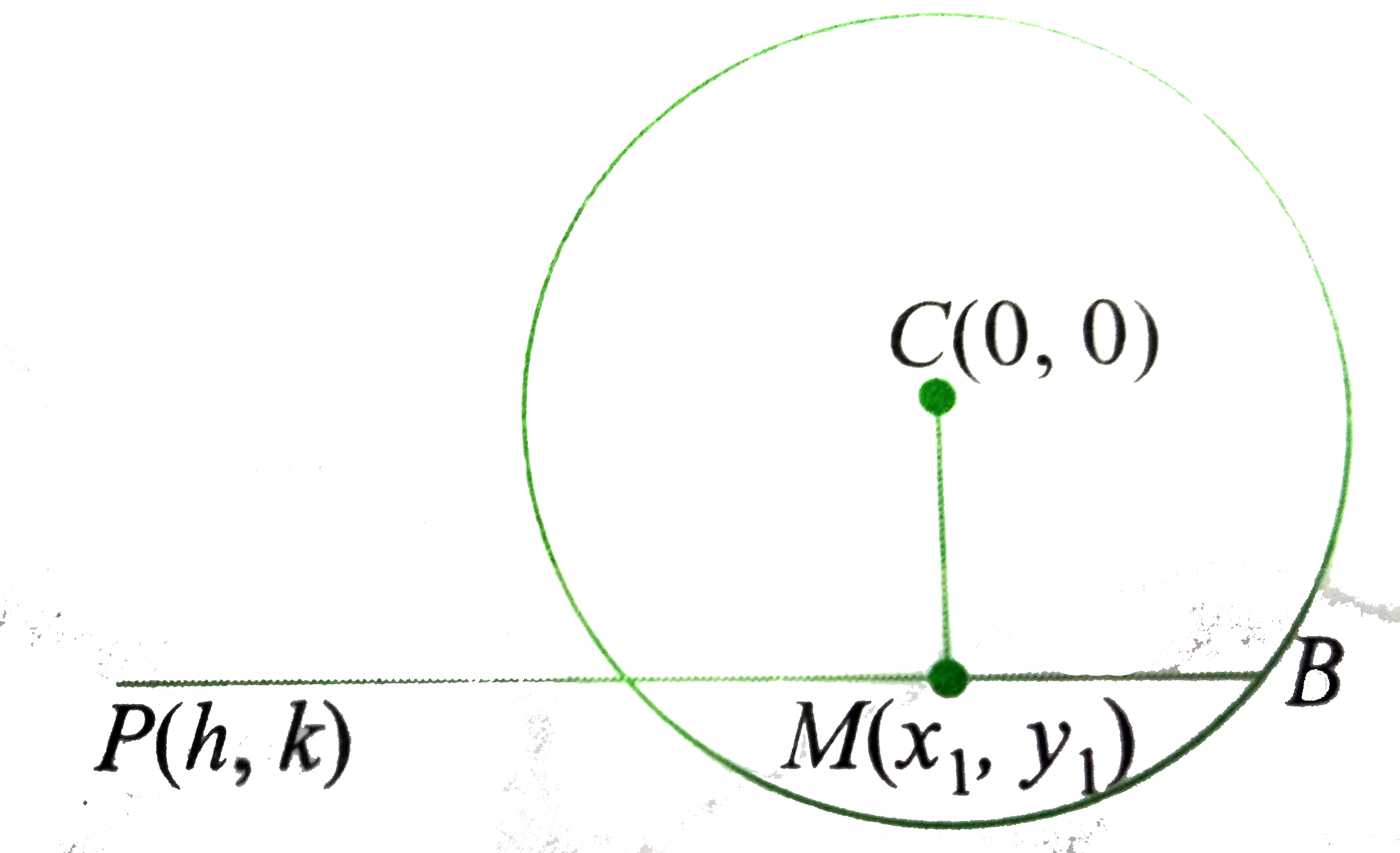
So, the locus of M is
x2+y2=hx+ky
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Excercises (Single Correct Answer Type)
109 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.19
1 Video
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The number of rational point(s) [a point (a, b) is called rational, if aandb both are rational numbers] on the circumference of a circle having center (π,e) is at most one (b) at least two exactly two (d) infinite
View Solutionabout to only mathematics
View SolutionFind the locus of the midpoint of the chord of the circle x2+y2−2x−2y=0 , which makes an angle of 1200 at the center.
View SolutionConsider set A={T(r+1)=.nCr(3)n−r(5x)r,r=0,1,23,…..,n}. Match the following lists :

View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Area of triangle OPR when θ=π/4 is
View SolutionLocus of the mid points of the chords of the circle x2+y2=a2 which pass through the fixed point (h,k) is x2+y2+2hx+2ky=0 x2+y2−2hx−2ky=0 x2+y2+hx+ky=0 x2+y2−hx−ky=0 x2+y2+hx−ky=0
View SolutionThrough a fixed point (h,k) secants are drawn to the circle x^(2)+y^(2)=r^(2). Then the locus of the mid-points of the secants by the circle is
View SolutionIf the line hx+ky=(1)/(a) touches the circle x^(2)+y^(2)=a^(2) then the locus of (h,k) is circle of radius
View SolutionThrough a fixed point (h,k), secant are drawn to the circle x2+y2=r2. Show that the locus of the midpoints of the secants by the circle is x2+y2=hx+ky.
View SolutionThe locus of the point P(h,k) for which the line hx+ky=1 touches the circle x2+y2=4, is
View SolutionIf the line hx + ky = 1 touches x2+y2=a2, then the locus of the point (h, k) is a circle of radius
View SolutionThrough a fixed point (h, k) secants are drawn to the circle x2+y2=a2 . The locus of the mid points of the secants intercepted by the given circle is
View Solutionएक नियत बिंदु (h,k) से वृत्त x2+y2=r2 पर एक छेदक रेखा (secant) खींची जाती है। दिखाइए की वृत्त पर खींची गई छेदक रेखाओं के मध्य-बिंदु का बिन्दुपथ x2+y2=hx+ky है।
View SolutionThrough a fixed point (h,k) secants are drawn to the circle x2+y2=r2. Show that the locus of the mid points of the position of the secants intercepted by the circle is x2+y2=hx+ky.
View SolutionThrough a fixed point (h, k) secants are drawn to the circle x2+y2=r2. Then the locus of the mid-points of the secants by the circle is
View Solution

