To divide a line segment AB in the ratio 5:6, draw a ray AX such that ∠BAX is an acute angle, the draw a ray BY parallel to AX and the points A1,A2,A3,….. and B1,B2,B3,….. are located to equal distances on ray AX and BY, respectively. Then, the points joined are
A5 and B6
A6 and B5
A4 and B5
A5 and B4
The correct Answer is:A
(a) Given , a line segment AB and we have to divide it in the ratio 5:6.
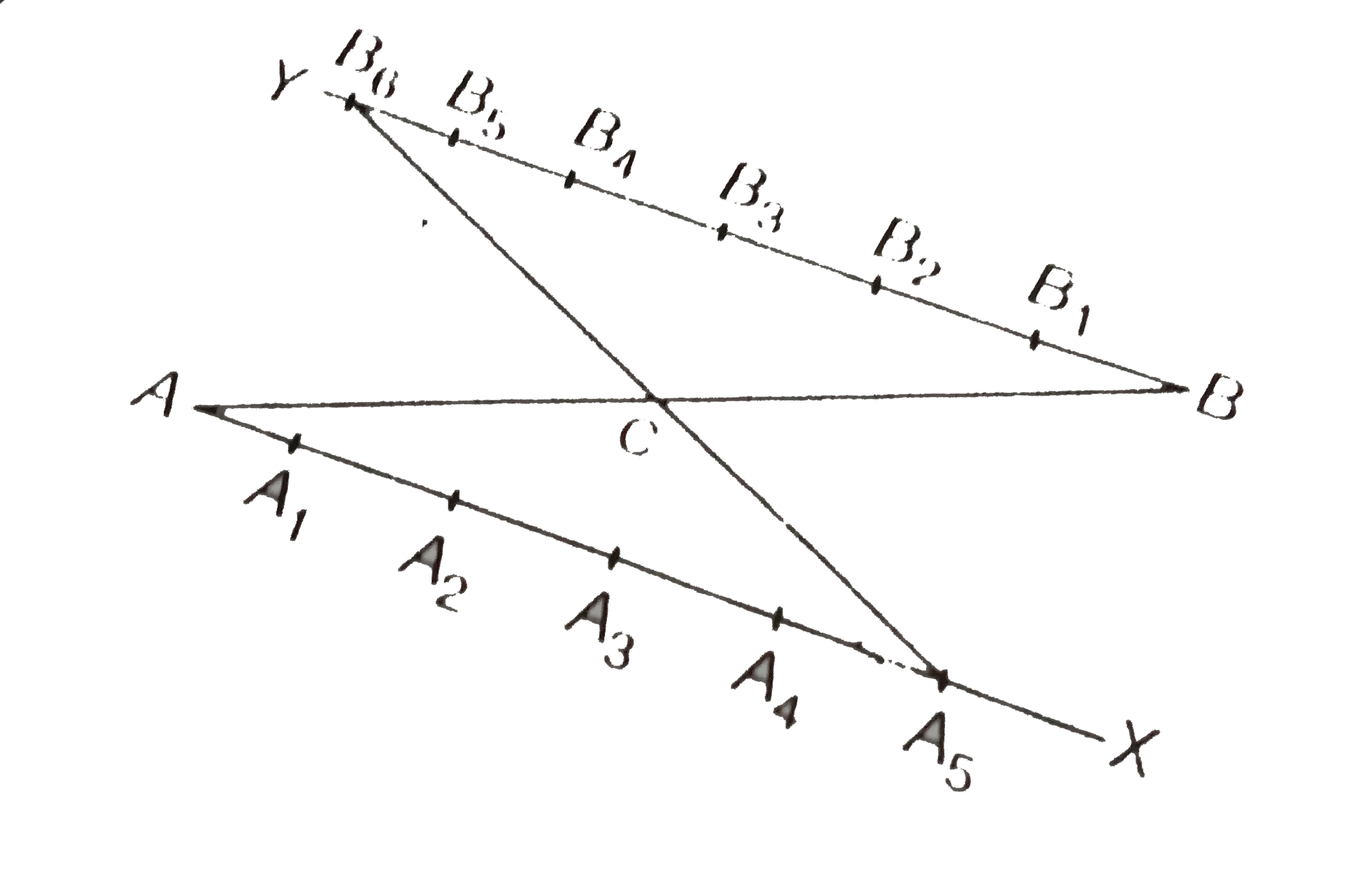
Steps of construction
1. Draw a AX making an acute ∠BAX.
2. Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.
3. Now, locate the points A1,A2,A3,A4 and A5(m=5) on AX and B1,B2,B3,B4,B5 and B6s(n=6) such that all the points are at equal distance from each other.
4. Join B6A5. Let it intesect AB at a point C.
Then, AC:BC=5:6
Similar Questions
Divide a line segment AB in the ratio 4:5, the points A1,A2,A3,....andB1,B2,B3,.... are located at equal distances on the ray AX and BY respectively. Which two points should be joined to divide a line segment?
View SolutionTo divide a line segment AB in the ratio 4:7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1,A2,A3,….. are located at equal distance on the ray AX and the point B is joined to
View Solution
Knowledge Check
To divide a line segment AB in the ratio 4:7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1,A2,A3,….. are located at equal distance on the ray AX and the point B is joined to
AA12BA11CA10DA9To divide a line segment AB in the ratio 2:5, first a ray AX is drawn, so that BAX is an acute angle and then at equal distance points are marked on the ray AX such that the minimum number of these point is:
A2B5C4D7To divide a line segment AB in the ratio 5:7, first a ray AX is drawn, so that ∠BAX is an acute angle and then at equal distances point are marked on the ray AX such that the minimum number of these points is
A8B10C11D12
Divide a line segment AB in the ratio 4:5, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1,A2,A3, ........ are located at equal distances on the ray AX which should be joined to B?
View SolutionIn the figure, if B1,B2,B3, and A1,A2,A3,….. have been marked at equal distances. In what ratio C divides AB?
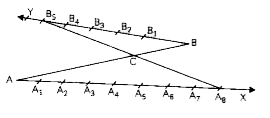
View SolutionTo divide a line segment BC internally in the ratio 3 : 5, we draw a ray BX such that ∠ CBX is an acute angle. What will be the minimum number of points to be located at equal distances, on ray BX?
View SolutionTo divide a line segment AB in the ratio 5:7, first a ray AX is drawn, so that ∠BAX is an acute angle and then at equal distances point are marked on the ray AX such that the minimum number of these points is
View SolutionDivide a line segment AB in the ratio 3:7, What is the minimum number of points marked on a ray AX at equal distances?
View Solution
