Two chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
We know that the perpendicular bisector of any chord of a circle always passes through its centre.
Since l is the perpendicular bisector of AB, l passes through the centre O of the circle.
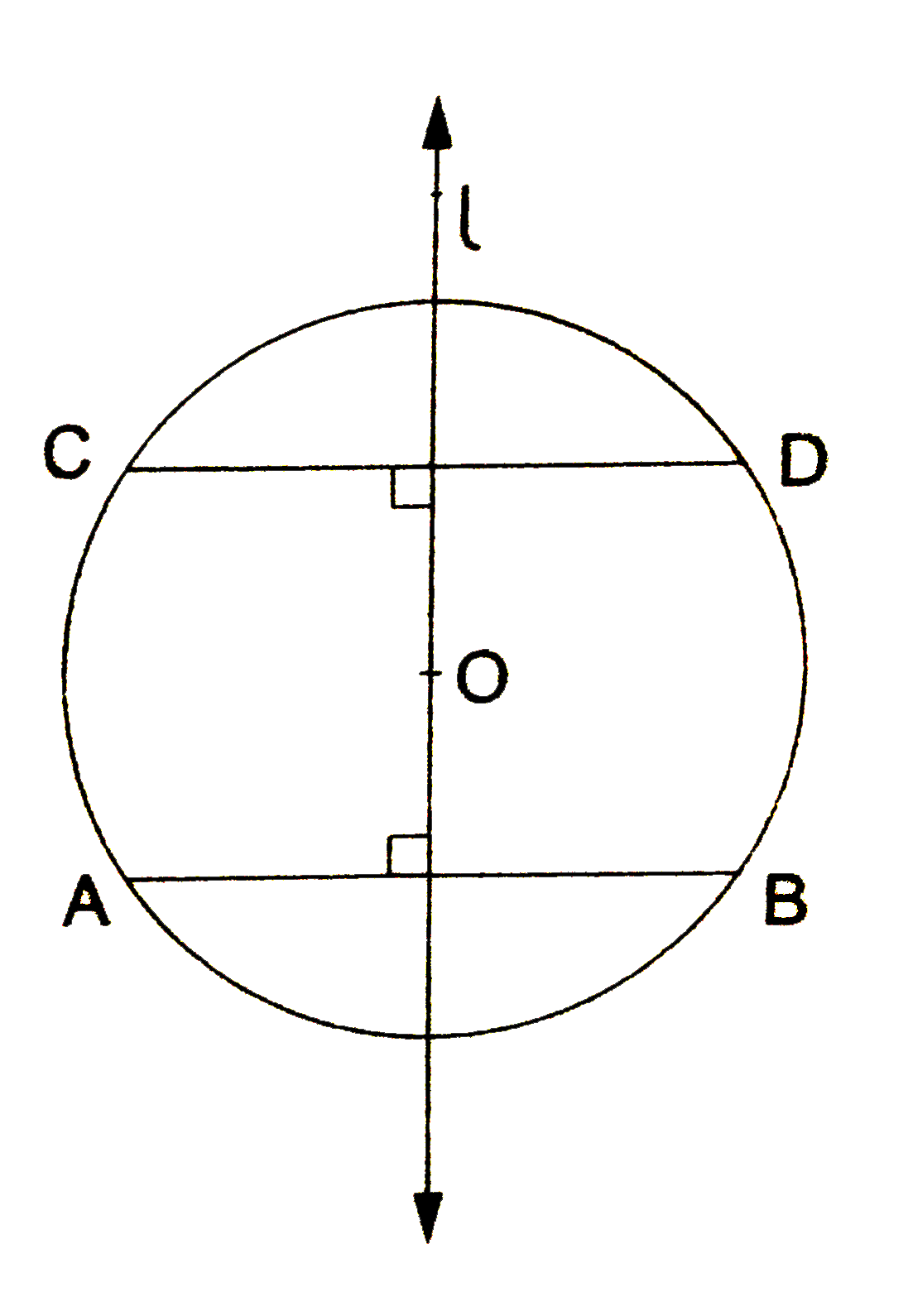
Now, l⊥ AB and AB∣∣CD⇒l⊥CD
Thus, l⊥CD and passes through the centre of the circle.
But, the perpendicular from the centre ofa circle to a chords bisects the chord.
∴ l must bisect the chord CD.
Similar Questions
Two chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB . Show that l bisects CD.
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA
View SolutionTwo lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionIn Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D and AP is the perpendicular bisector of BC
View SolutionIn Figure, if AD is the bisector of LA , show that: AB>BD (ii) AC>CD
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View Solution
