Two circle with radii r1 and r2 respectively touch each other externally. Let r3 be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is true
1√a−1√b=1√c
c=2aba+b
1√a+1√b=1√c
c=2ab√a+√b
The correct Answer is:3
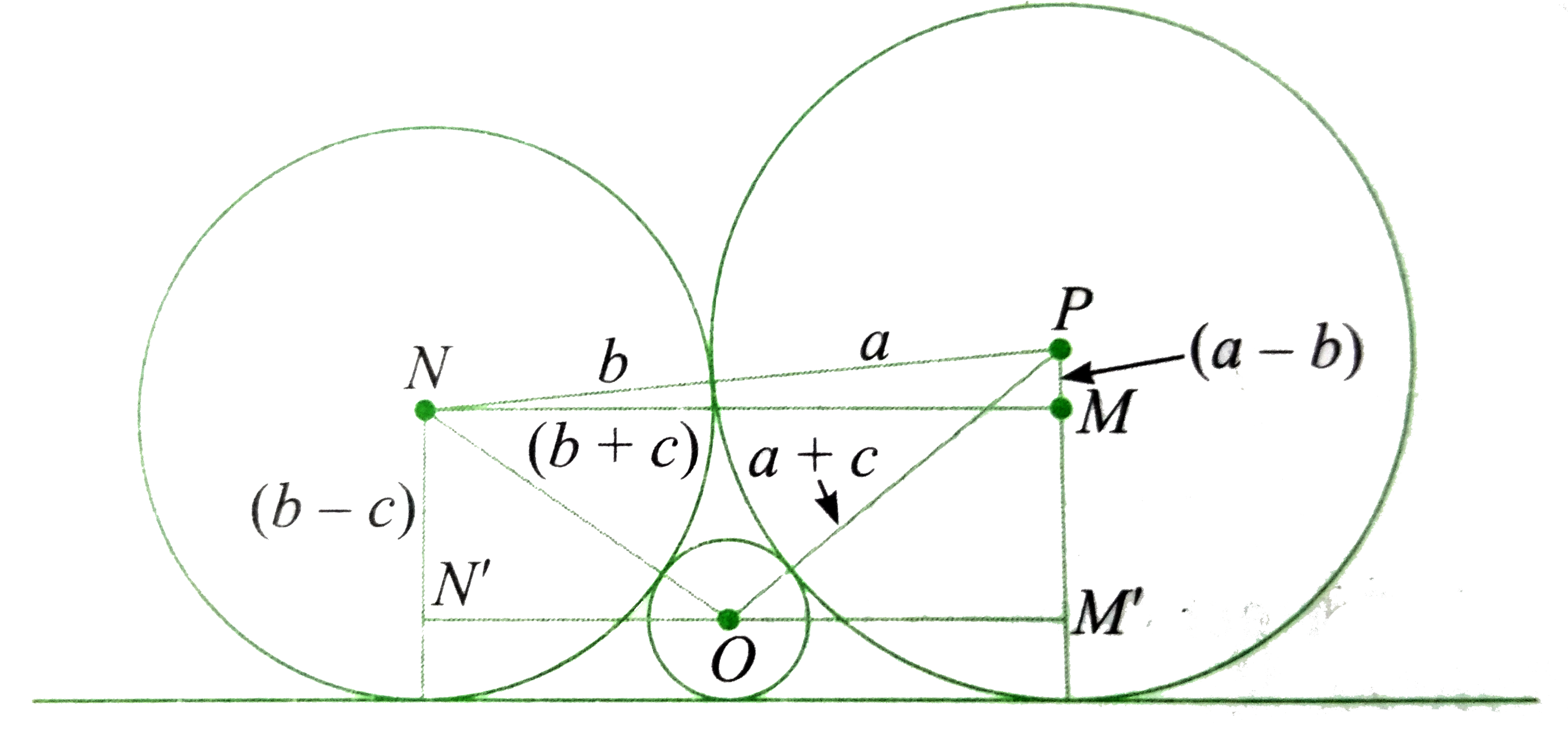
∵M'N'=MN
Now, MN=√(a+b)2+(a−b)2=√4ab
N'O=√(b+c)2−(b−c)2=√4bc
M'O=√(b+c)2−(a−c)2=√4ac
Now, N'O+M'O=MN
⇒2√ab=2√bc+2√ac
Dividing by 1√abc, we get
1√c=1√a+1√b
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionTwo fixed circles with radii r1andr2,(r1>r2) , respectively, touch each other externally. Then identify the locus of the point of intersection of their direction common tangents.
View SolutionTwo circles of radii r_(1) and r_(2)(r_(1)>r_(2)) touch each other exterally.Then the radius of circle which touches both of them externally and also their direct common tangent is (A) ( sqrtr_(1)+sqrt(r)_(2))^(2) (B) sqrt(r_(1)r_(2))(C)(r_(1)+r_(2))/(2) (D) (r_(1)-r_(2))/(2)
View SolutionTwo circles of radii r_(1) and r_(2), are both touching the coordinate axes and intersecting each other orthogonally.The value of (r_(1))/(r_(2)) (where r_(1)>r_(2)) equals -
View SolutionLet ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing thorugh B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
r1r2 equals
View SolutionLet ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing through B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
Minimum value of (r1+r2 equals
View SolutionThree circles C_(1),C_(2),C_(3) with radii r_(1),r_(2),r_(3)(r_(1)ltr_(2)ltr_(3)) respectively are given as r_(1)=2 , and r_(3)=8 they are placed such that C_(2) lines to the right of C_(1) and touches it externally C_(3) lies ot the right of C_(2) and touches it externally. There exist two stratight lines each of whic is a direct common tangent simultaneously to all the three circles then r_(2) is equal to
View SolutionTwo circle with radii r1 and r2 respectively touch each other externally. Let r3 be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is true
View SolutionThe locus of the centre of a variable circle touching two circles of radii r1, r2 externally , which also touch eath other externally, is conic. If r1r2=3+2√2, then eccentricity of the conic, is
View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
View SolutionTwo circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
View SolutionCircles of radii 36 and 9 touches externally. The radius of the circle which touches the two circles externally and also their common tangent is
View Solution

