Two isosceles triangles have equal vertical angles and their areas are in the ratio 16:25. Then, the ratio of their corresponding height is :
4:5
5:4
3:6
5:7
To solve the problem, we need to find the ratio of the corresponding heights of two isosceles triangles given that their areas are in the ratio of 16:25.
1. Understanding the Area Ratio:
The areas of two triangles are given in the ratio 1625. Let's denote the areas of triangle ABC and triangle DEF as A1 and A2 respectively. Thus, we have:
A1A2=1625
2. Using the Area Formula:
The area of a triangle can be expressed as:
A=12×base×height
For isosceles triangles, if we denote the bases of triangles ABC and DEF as b1 and b2, and their corresponding heights as h1 and h2, we can write:
A1=12×b1×h1
A2=12×b2×h2
3. Setting Up the Ratio of Areas:
From the area expressions, we can set up the ratio:
A1A2=12×b1×h112×b2×h2=b1×h1b2×h2
Therefore, we have:
b1×h1b2×h2=1625
4. Considering the Bases:
Since the triangles are isosceles and have equal vertical angles, the bases are proportional to the heights. Thus, we can assume that the ratio of the bases b1b2 is equal to the ratio of the heights h1h2. Let:
b1b2=kandh1h2=k
5. Substituting the Ratios:
Substituting b1=k⋅b2 into the area ratio gives us:
k⋅b2⋅h1b2⋅h2=1625
Simplifying this, we find:
k⋅h1h2=1625
6. Finding the Height Ratio:
Since k=h1h2, we can substitute this into the equation:
k2=1625
Taking the square root of both sides gives:
k=45
Therefore, the ratio of the corresponding heights h1h2 is:
h1h2=45
Final Answer:
The ratio of the corresponding heights of the two triangles is 45.
The areas of two triangles are given in the ratio 1625. Let's denote the areas of triangle ABC and triangle DEF as A1 and A2 respectively. Thus, we have:
A1A2=1625
The area of a triangle can be expressed as:
A=12×base×height
For isosceles triangles, if we denote the bases of triangles ABC and DEF as b1 and b2, and their corresponding heights as h1 and h2, we can write:
A1=12×b1×h1
A2=12×b2×h2
From the area expressions, we can set up the ratio:
A1A2=12×b1×h112×b2×h2=b1×h1b2×h2
Therefore, we have:
b1×h1b2×h2=1625
Since the triangles are isosceles and have equal vertical angles, the bases are proportional to the heights. Thus, we can assume that the ratio of the bases b1b2 is equal to the ratio of the heights h1h2. Let:
b1b2=kandh1h2=k
Substituting b1=k⋅b2 into the area ratio gives us:
k⋅b2⋅h1b2⋅h2=1625
Simplifying this, we find:
k⋅h1h2=1625
Since k=h1h2, we can substitute this into the equation:
k2=1625
Taking the square root of both sides gives:
k=45
Therefore, the ratio of the corresponding heights h1h2 is:
h1h2=45
The ratio of the corresponding heights of the two triangles is 45.
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 2 BASICBook:X BOARDSChapter:QUESTION PAPER 2022 TERM 1 SET 2 BASICExercise:SECTION B
Explore 20 Videos
- QUESTION PAPER 2022 TERM 1 SET 2 BASICBook:X BOARDSChapter:QUESTION PAPER 2022 TERM 1 SET 2 BASICExercise:SECTION C (Case Study Based Question)
Explore 10 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBook:X BOARDSChapter:QUESTION PAPER 2022 TERM 1 SET 1 STANDARDExercise:SECTION-C (CASE STUDY)
Explore 10 Videos
- QUESTION PAPER 2022 TERM 1 SET 2 STANDARDBook:X BOARDSChapter:QUESTION PAPER 2022 TERM 1 SET 2 STANDARDExercise:SECTION-C
Explore 10 Videos
Similar Questions
Find the HCF of 30,72 and 432.
View SolutionA rough co-ordinate map of Lahiri's locality is shown below :
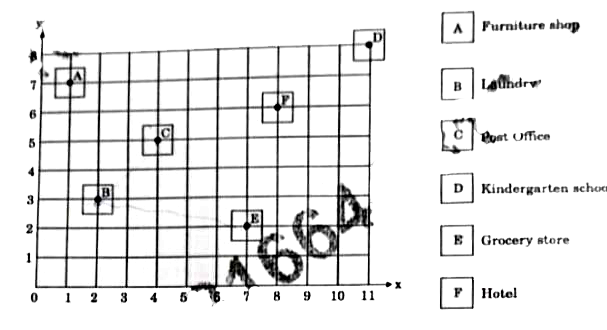
The coordinates of the grocery store are :
View SolutionA book store shopkeeper gives books on rent for reading. He has variety of books in his store related to fiction , stories and quizzes etc. He takes a fixed charge for the first two days and an additional charges for subsequent day . Amruta paid Rs 22 for a book and kept for 6 days, while Radhika paid Rs 16 for keeping the books for 4 days.

Assume that the fixed charge be rs x and additional charge (per day) by Rs y.
Based on the above information answer and four of the following questions:
The situation of amount paid by Radhika is algebraically repesented by .
View SolutionA car moves on a highway . The path it traces is given below
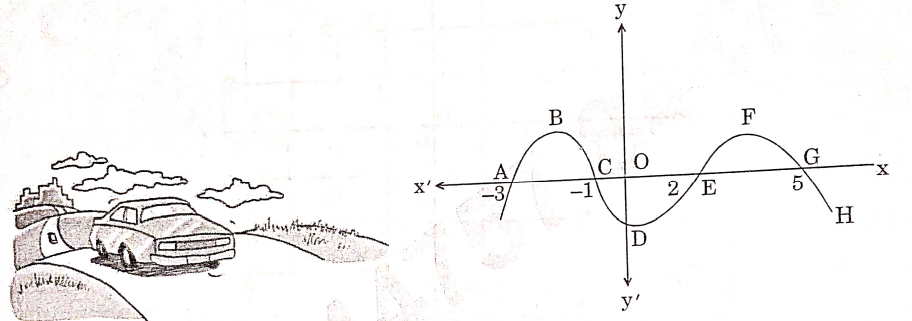
Based on the above information , answer the following questions :
What is the shape of the curve EFG ?
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 16:25 . Find the ratio of their corresponding heights.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 36:25 . Find the ratio of their corresponding heights.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 9:16 . Find the ratio of their corresponding heights.
View SolutionTwo isosceles triangles have their corresponding angles equal and their areas are in the ratio 25:36. The ratio of their corresponding heights is
View Solutionदो समद्विबाहु त्रिभुजों की शीर्षकोण समान है और उनके क्षेत्रफलो के अनुपात 16 : 25 है तो उनकी संगत ऊँचाइयाँ के अनुपात ज्ञात कीजिए |
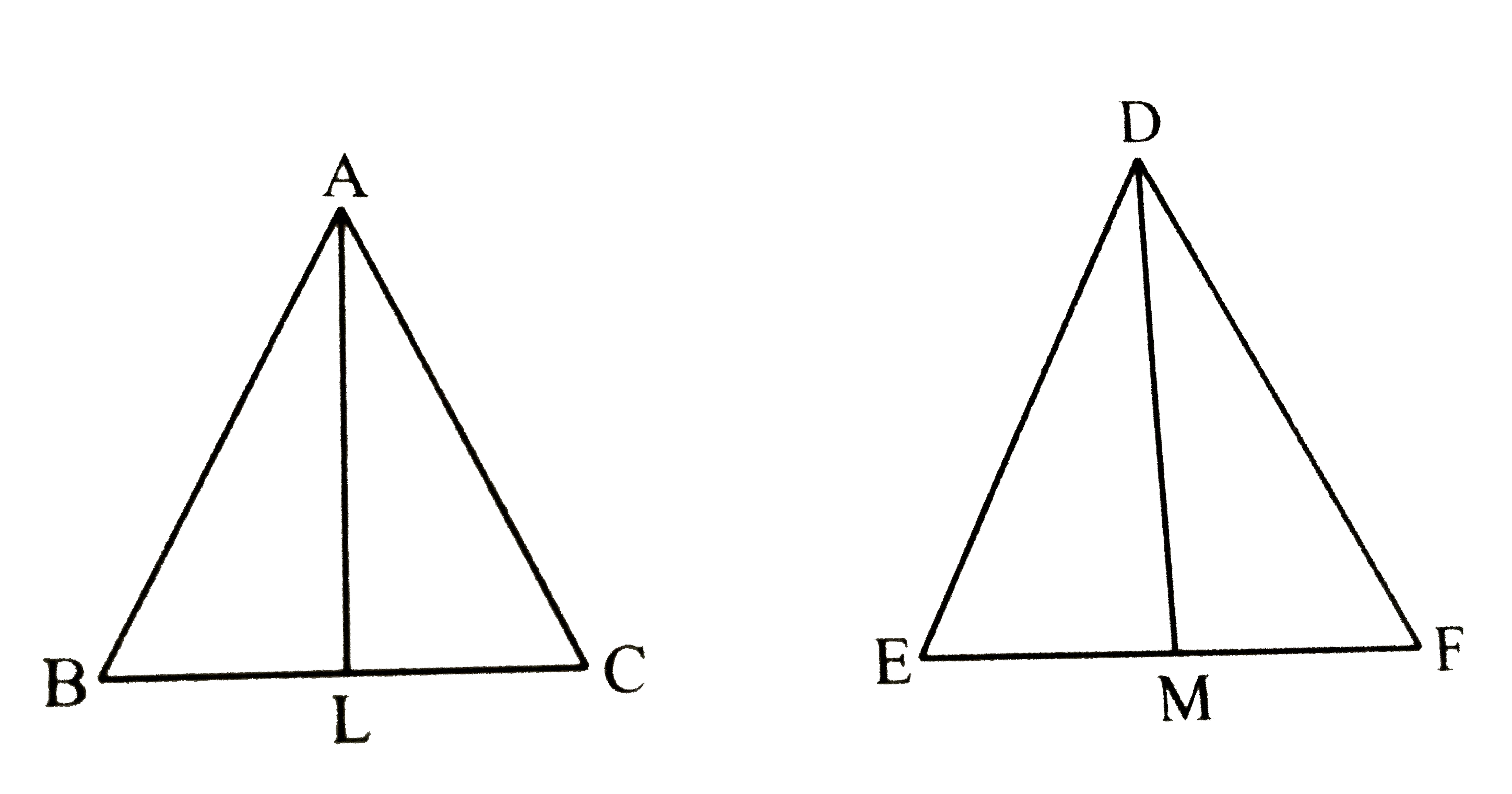
View Solutionदो समद्विबाहु त्रिभुजों के शीर्षकोण बराबर हैं और उनके क्षेत्रफल 25:36 के अनुपात में हैं । उनकी संगत ऊँचाइयों में अनुपात ज्ञात कीजिए ।
View SolutionTwo isosceles triangles are having equal vertical angles and their areas are in the ratio 9:16. Find the ratio of their corresponding altitudes.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 16:25 . Find the ratio of their corresponding heights.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 36:25 . Find the ratio of their corresponding heights.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding altitudes.
View Solutionदो समद्विभाहु त्रिभुजों के शीर्ष कोण बराबर हैं, और उनके क्षेत्रफल 16 : 25 के अनुपात में हैं। उनकी संगत ऊँचाइयों का अनुपात ज्ञात कीजिए।
View Solutionदो समद्विबाहु त्रिभुजों के शोर्ष कोण बराबर है और उनके क्षेत्रफलों में 9:16 का अनुपात है। उनकी सांगत भुजाओं का अनुपात है-
View Solution