Two variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a, M and N are the mid-points of AB and BC respectively such that line joining MN intersect the circle at P and Q where P is closer to AB and O is the centre of the circle.
∠OAB is
90∘
120∘
60∘
150∘
The correct Answer is:3
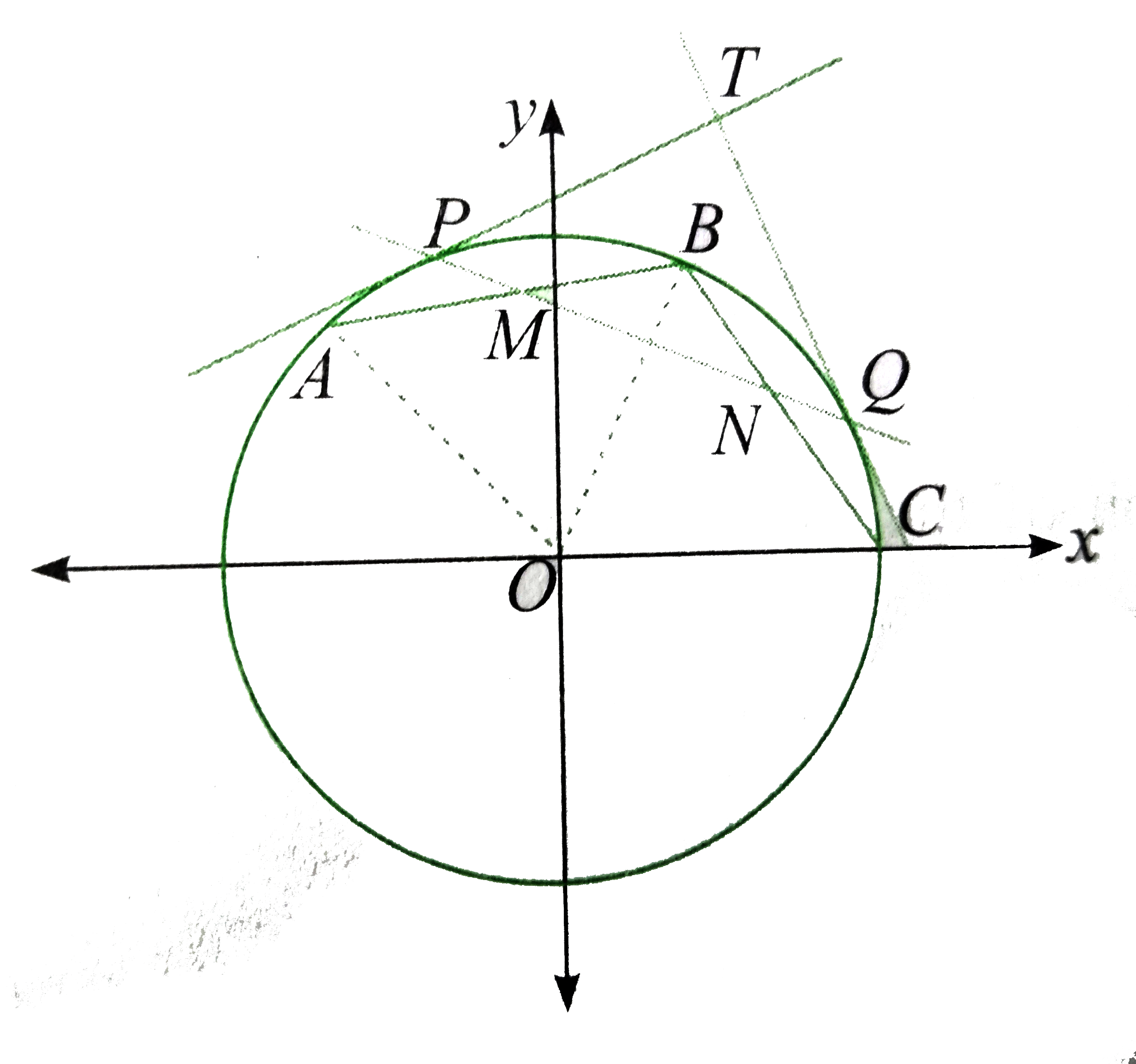
Let T be the point of intersection of tangents .
Since ∠AOC=120∘, the angle between the tangents is 60∘
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:NUMERICAL VALUE TYPE
Explore 21 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:ARCHIVES (JEE MAIN)
Explore 1 Video
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Linked Comprehension Type (For Problem 1-3)
Explore 3 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Let the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2+gx+fy+7=0 , then the value of |f+g| is__________
View SolutionIf P and Q are the points of intersection of the circles x2+y2+3x+7y+2p=0 and x2+y2+2x+2y−p2=0 then there is a circle passing through P,Q and (1,1) for
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionConsider set A={T(r+1)=.nCr(3)n−r(5x)r,r=0,1,23,…..,n}. Match the following lists :

View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Area of triangle OPR when θ=π/4 is
View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
∠OAB is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The angle between the tangents at A and C is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
View SolutionIn circle AOD is diameter with centre of circle O and AB,BC,CD are equal chord then angle suntened by chord BC at centre is
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a ,then locus of point of intersection of tangents at A and C is a circle of radius λa, where λ is
View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionTwo variable chords AB and BC of a circle x2+y2=a2 are such that AB=BC=a. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is
View Solution
