What are the zeroes of the polynomial (x2−9)?
(3, 0)
(3, -3)
(0, 3)
(3, 3)
The correct Answer is:B
To find the zeroes of the polynomial x2−9, we need to determine the values of x for which the polynomial equals zero.
1. Set the polynomial equal to zero:
x2−9=0
2. Rearrange the equation:
x2=9
3. Take the square root of both sides:
x=±√9
4. Calculate the square root:
x=±3
5. Write the zeroes:
The zeroes of the polynomial x2−9 are:
x=3andx=−3
Final Answer:
The zeroes of the polynomial x2−9 are 3 and −3.
x2−9=0
x2=9
x=±√9
x=±3
The zeroes of the polynomial x2−9 are:
x=3andx=−3
The zeroes of the polynomial x2−9 are 3 and −3.
Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section - A
7 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section - B
4 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section -C
7 Videos
- SAMPLE QUESTION PAPERBOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE QUESTION PAPEREXERCISE - Section -C
5 Videos
Similar Questions
The 4th term of an A.P. is equal to 3 times the first term and 7th term excess with the 3rd term by 1. Find its nth term.
View SolutionIn a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
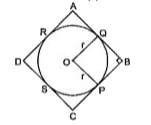
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).
View SolutionThe internal and external radii of a hollow spherical shell are 3 cm and 5 cm-respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder.
View SolutionIf alpha and beta are the zeroes of the polynomial x^(2)+6x+9 then form a polynomial whose zeroes are -alpha and -beta
View Solutionयदि बहुपद f(x)=2x3+6x2−4x+9 के दो शुन्यकों का गुणनफल 3 हो, तो बहुपद का तीसरा शून्यक है :
View Solutionयदि बहुपद x3+x2−9x−9 के दो शून्यक 3 तथा -3 हों तो इसका तीसरा शून्यक है :
View SolutionCheck wheather -3 and 3 are the zeroes of the polynomial x2−9.
View SolutionThe zeroes of the polynomial p(x)=4x2−12x+9 are
View SolutionThe zeros of the polynomial p(x)=x2−9 are
View Solutionबहुपद x2−6x+9 का शून्यक है-
View SolutionThe zero of the polynomial p(x) = -9x + 9 is:
View SolutionCheck whether −3 and 3 are the zeroes of the polynomial x2−9.
View SolutionCheck whether −3 and 3 are the zeroes of the polynomial x2−9.
View SolutionCheck whether −3 and 3 are the zeroes of the polynomial x2−9.
View SolutionCheck whether −3 and 3 are the zeroes of the polynomial x2−9.
View Solution
