What is the number of sides of a polygen in which the sum of the degree measure of the interior angles is 4 times the sum of the degree measures of the exterior angles?
10
12
14
No such polygon exist
The correct Answer is:A
To solve the problem, we need to find the number of sides n of a polygon where the sum of the degree measures of the interior angles is 4 times the sum of the degree measures of the exterior angles.
1. Understand the formulas:
- The sum of the interior angles of an n-sided polygon is given by the formula:
Sum of interior angles=(n−2)×180∘
- The sum of the exterior angles of any polygon is always:
Sum of exterior angles=360∘
2. Set up the equation:
- According to the problem, the sum of the interior angles is 4 times the sum of the exterior angles. Therefore, we can write the equation:
(n−2)×180∘=4×360∘
3. Calculate the right side of the equation:
- Simplifying the right side:
4×360∘=1440∘
4. Substitute and simplify:
- Now we have:
(n−2)×180∘=1440∘
- To isolate n−2, divide both sides by 180∘:
n−2=1440∘180∘
- Calculating the division:
n−2=8
5. Solve for n:
- Add 2 to both sides to find n:
n=8+2=10
Conclusion:
The number of sides of the polygon is n=10.
- The sum of the interior angles of an n-sided polygon is given by the formula:
Sum of interior angles=(n−2)×180∘
- The sum of the exterior angles of any polygon is always:
Sum of exterior angles=360∘
- According to the problem, the sum of the interior angles is 4 times the sum of the exterior angles. Therefore, we can write the equation:
(n−2)×180∘=4×360∘
- Simplifying the right side:
4×360∘=1440∘
- Now we have:
(n−2)×180∘=1440∘
- To isolate n−2, divide both sides by 180∘:
n−2=1440∘180∘
- Calculating the division:
n−2=8
- Add 2 to both sides to find n:
n=8+2=10
The number of sides of the polygon is n=10.
Similar Questions
Knowledge Check
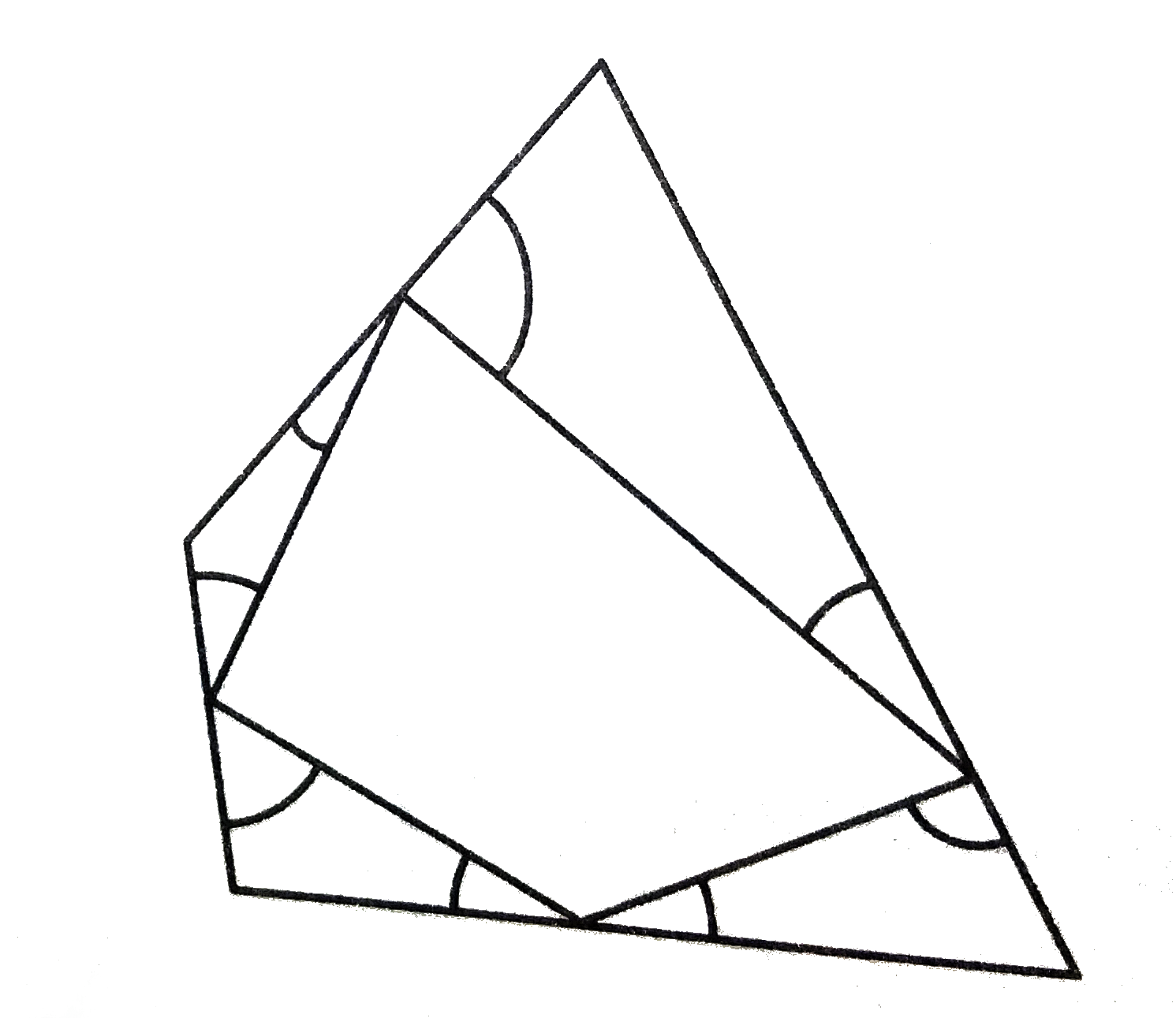
In the figure above, what is the sum of the degree measures of the marked angles?
A120B180C360DIt cannot be determined from the information given
In the figure above, what is the sum of the degree measures of all of the angles marked?A540B720C900D1080In this triangle, what is the degree measure of angle c ?
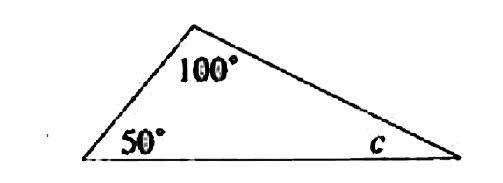 A17B20C30D40
A17B20C30D40
How many sides does a regular polygon have if the measure of an exterior angle is 24∘?
View SolutionFind the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
View SolutionHow many sides does a regular polygon have if the measure of an exterior angle is 240?
View SolutionThe angles of trinalge are in the ratio 2:3:4. What is the degree measures of the largest angle?
View Solution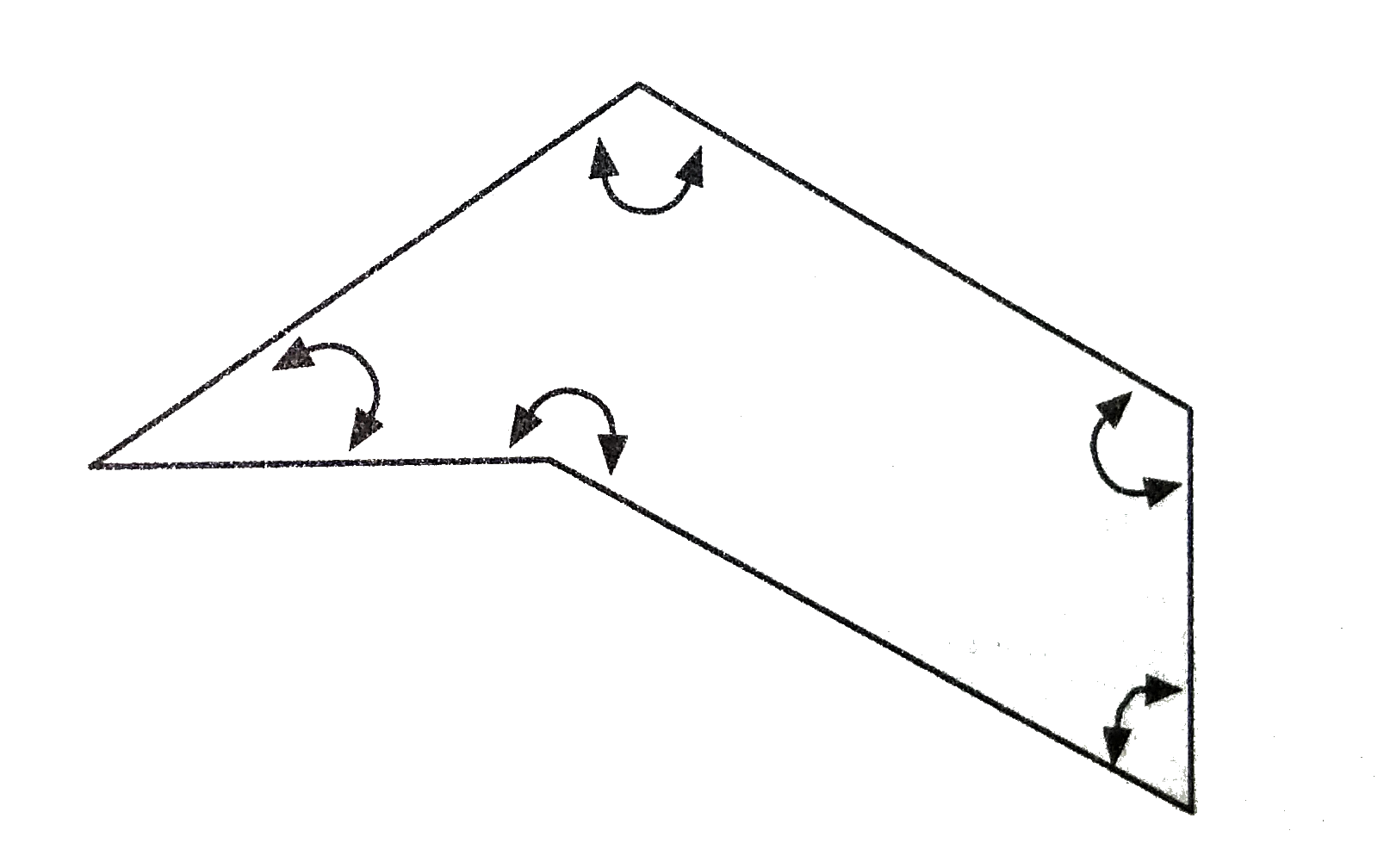
What is the total number of degrees of the marked angles?
View Solution