Complete Solutions to PROBLEM of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| PRADEEP | PROBLEM |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
Ammonia and oxygen react at high temperature as:
`4NH_(3) (g) + 5O_(2)(g) rarr 4NO(g) + 6H_(2)O (g)`
In an experiment, the rate of formation of `NO` is `3.6 xx 10^(-3) Ms^(-1)`. Calculate (a) the rate of disappearance of ammonia and (b) the rate of formation of water.
View SolutionThe reaction, `2N_(2)O_(s)(g)iff4NO_(2)(g)+O_(2)(g)` was studied in a closed vessel It was found that the concentration of `NO_(2)` increases by `2*0xx10^(-2)"mol "L^(-1)` in five seconds. Calculate
(i) the rate of reaction (ii) the rate of change of concentration of `N_(2)O_(5)`.
View SolutionFor an elementary, `2A+Bto3C`, the rate of appearance of C at time 't' is `1*3xx10^(-4)"mol "L^(-1)s^(-1)`. Calculate at this time (i) rate of the reaction (ii) rate of disappearance of A.
View SolutionFor the decomposition of dinitrogen pentoxide at `200^(@)C`,
`N_(2)O_(5)(g)toN_(2)O_(4)(g)+(1)/(2)O_(2)(g)`,
if the intial pressure is 14 mm and after 25 minutes of the reaction, total pressure of the gassous mixture is 133 mm, calculate the average rate of reaction in (a) atm `min^(-1)" "(b)" mol "L^(-1)s^(-1)`.
View SolutionFrom the concentrations of `C_(4)H_(9)Cl` (butyl chloride) at different times given below, calculate the average rate of the reaction:
`C_(4)H_(9)Cl +H_(2)Orarr C_(4)H_(9)OH+HCl`
during different intervals of time.
`{:(t//s,0,50,100,150,200,300,400,700,800),([C_(4)H_(9)Cl]//"mol"^(-1),0.100,0.0905,0.0820,0.0741,0.0671,0.0549,0.0439,0.0210,0.017):}`
View SolutionThe decompoistion of `N_(2)O_(5)` in `C CI_(4)` solution at `318 K` has been studied by monitoring the concentration of `N_(2)O_(5)` in the solution. Initially, the concentration of `N_(2)O` is `2.33 M` and after `184 min`, it is reduced to `2.08 M`. The reaction takes place according to the equation:
`2N_(2)O_(5) rarr 4NO_(2) + O_(2)`
Calculate the average rate of this reaction in terms of hours, minutes, and seconds. What is the rate of Production of `NO_(2)` during this period?
View SolutionFor a homogeneous decomposition of `N_(2)O_(5)` into `NO_(2)" and "O_(2)`,
`2N_(2)O_(5)(g)to4NO_(2)(g)+O_(2)(g)," rate "=(-(1)/(2)Delta[N_(2)O_(5)])/(Deltat)=k[N_(2)O_(5)]`
Find out the order with respect to `N_(2)O_(5)`.
View SolutionCalculate the overall order of a reaction which has the rate expression :
(a) Rate `=k[A]^(1//2)[B]^(3//2)" "(b)" Rate "=k[A]^(3//2)[B]^(-1)`
View SolutionThe rate law for a reaction is found to be : Rate `=k [NO_(2)^(-) ][ I^(-)][H^(+)]^(2)`
How would the rate of reaction change when (i) Concentration of `H^(+)` is doubled
(ii) Concentration of `I^(-)` is halved (iii) Concentration of each of `NO_(2)^(-),I^(-)` and `H^(+)` are tripled?
View SolutionThe rate of a gaseous reaction is halved when the volume of the vessel is doubled. What is the order of reaction ?
View SolutionFor the reaction, `2NH_(3)rarr N_(2)+3H_(2)`
if `(-d[NH_(3)])/(dt)=k_(1)[NH_(3)]`,
`(d[N_(2)])/(dt)=k_(2)[NH_(3)], (d[H_(2)])/(dt)=k_(3)[NH_(3)]`
then the relation between `k_(1), k_(2)` and `k_(3)` is
View SolutionIdentify the reaction order from each of the following rate constant :
(i) `k=2*3xx10^(-5)" litre "mol^(-1)sec^(-1)" "(ii) k=3*1xx10^(-4)sec^(-1)`
(iii) `k=9*3xx10^(-4)"mol litre"^(-1)sec^(-1)`
View SolutionDuring the decomposition of a gas on the surface of a solid catalyst, the pressure of the gas at different times was observed to be as follows :
`{:(t//s,,," "0,,," "100,,," "200,,," "300),(p//Pa,,,5*00xx10^(3),,,4*20xx10^(3),,,3*40xx10^(3),,,2*60xx10^(3)):}`
Calculate order, rate constant and half-life period of this reaction.
View SolutionThe rate of decomposition of `NH_3` on platinum surface, `2NH_(3) (g) overset(Pt) (to) N_(2) (g) + 3H_(2) (g)` is rate `=k` order with `k = 2.5 xx 10^(-4)" mol L"^(-1)" s"^(-1)`. What are the rates of production of `N_2 and H_2`?
View SolutionThe rate constant for a reaction of zero order in A is `0.0030 mol L^(-1)s^(-1)`. How long will take for the initial concentration to fall from 0.10 M to 0.075 M?
View SolutionThe rate constant for a first order reaction is `60s^(-1)`. How much time will it take to reduce the initial concentrationof the reactant to its `1//16th` value ?
View SolutionThe half-life period of a first order reaction is 60 minutes. What percentage will be left after 240 minutes ?
View SolutionThe experimental data for the decomposition of `N_(2)O_(5)[2N_(2)O_(5)to4NO_(2)+O_(2)]` in gas phase at 318 K are given below :
`{:(t//s,,0,,400,,800,,1200,,1600,,2000,,2400,,2800,,3200),(10^(2)xx[N_(2)O_(5)]//molL^(-1),,1*63,,1*36,,1*14,,0*93,,0*78,,0*64,,0*53,,0*43,,0*35):}`
`{:("(i) Plot "[N_(2)O_(5)]" against time.",,,,"(ii) Find the half-life period for the reaction."),("(iii) Draw a graph between "log[N_(2)O_(5)]" and t.",,,,"(iv) What is rate law ?"):}`
(v) Calculate the rate constant. (vi) Calculate the half-life period from k and compare it with (ii).
View SolutionThe rate of formation of a dimer in a second order dimerization reaction is `9.5 xx 10^(-5) mol L^(-1) s^(-1)` at `0.01 mol L^(-1)` monomer concentration. Calculate the rate constant.
View SolutionThe following rate data were obtained at 303K for the following reaction :
`2A+BtoC+D`
`{:("Experiment",,,[A]//"mol "L^(-1),,,[B]//"mol "L^(-1),,,"Initial rate of formation of "D//"mol "L^(-1)min^(-1)),(I,,,0*1,,,0*1,,,6*0xx10^(-3)),(II,,,0*3,,,0*2,,,7*2xx10^(-2)),(III,,,0*3,,,0*4,,,2*88xx10^(-1)),(IV,,,0*4,,,0*1,,,2*4xx10^(-2)):}`
What is the rate law ? What is the order with respect to each reactant and the overall order ? Also calculate the rate constant and write its units.
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentration of A and B as given below:
`{:(A//M,0.20,,0.20,0.40),(B//M,0.30,,0.10,0.05),(r_(0)//M s^(-1),5.07xx10^(-5),,5.07xx10^(-5),7.6xx10^(-5)):}`
View SolutionThe rate of a reaction starting with initial concentration of `2 xx 10^(-3)` and `1 xx 10^(-3) M` are equal to `2.40 xx 10^(-40)` and `0.60 xx 10^(-4) M s^(-1)`, respectively. Calculate the order of reaction w.r.t. reactant and also the rate constant.
View SolutionThe half-life periof of a substance is `50 min` at a certain initial concentration. When the concentration is reduced to one-half of its initial concentration, the half-life periof is found to be `25 min`. Calculate the order of reaction.
View SolutionPredict the order of the reaction in the given plots :

View Solutionform the following data for the decompoistion of `N_(2)O_(5)` in carbon tertrachloride solution at `321 K`, show that the reaction is of the first order and calculate the rate constant.
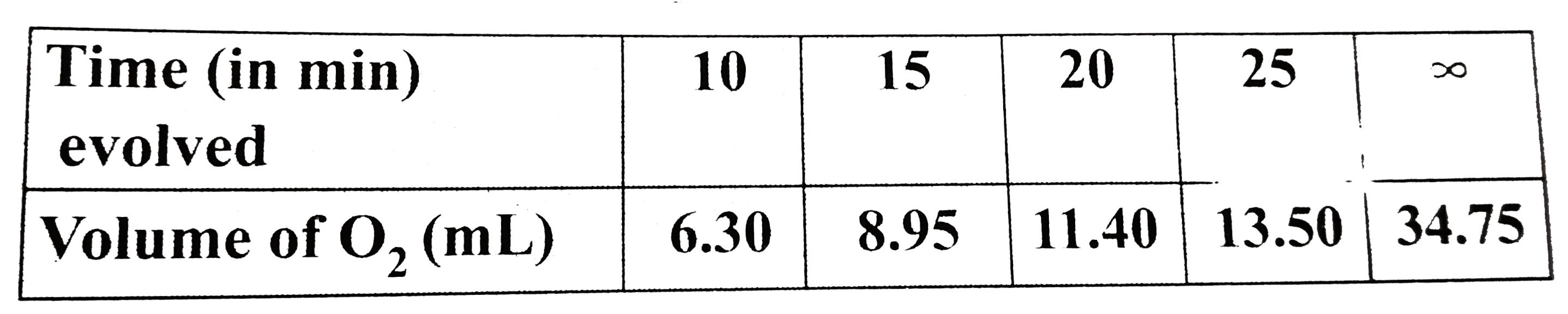
View SolutionThe decomposition of `N_(2)O_(5)` in `CCl_(4)` solution follows the first order rate law. The concentrations of `N_(2)O_(5)` measured at different intervals are given below :
`{:("Time in seconds (t)",,,0,,,80,,,160,,,410,,,600,,,1130,,,1720),(["N"_(2)"O"_(5)]"mol"//"L",,,5.5,,,5.0,,,4.8,,,4.0,,,3.4,,,2.4,,,1.6):}`
Calculate the rate constant at t = 410 s and t = 1130 s. What do these results show ?
View SolutionFrom the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order :
`{:(t,,,0,,,10,,,20),(x,,,46.1,,,29.8,,,19.3):}`
where t is the time in minutes and x is the volume of standard `KMnO_(4)` solution in `"cm"^(3)` required for titrating the same volume of the reaction mixture.
View Solution1.0 ml of ethyl acetate was added to 25 ml of N/2 HCl. 2 ml of the mixture were withdrawn from time to time during the progress of the hydrolysis of the ester and titrated against standard NaOH solution. The amount to NaOH required for titration at various intervals is given below :
`{:("Time (min)",,,:,,,0,,,20,,,75,,,119,,,183,,,oo),("NaOH used (ml)",,,:,,,20.24,,,21.73,,,25.20,,,27.60,,,30.22,,,43.95):}`
The value at `oo` time was obtained by completing the hydrolysis on boiling. Show that it is a reaction of the first order and find the average value of the velocity constant.
View SolutionThe hydrolyiss of methyl acetate in aqueous solution is has been studied by titrating the liberated acetic acid against `NaOH`. The concentration of ester at different times is given below:
`|{:("t (min)",0,30,60,90),(C (Mol L^(-1)),0.8500,0.8004,0.7538,0.7096):}|`
Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant `(55 mol L^(-1))` during the course of the reaction . What is the value of `k'` in the equation ?
Rate `= k'[CH_(3)COOCH_(3)][H_(2)O]`
View SolutionThe inverison of cane sugar was studied is `HCl` at `298 K`. The following polarimetric readings were obtained at different intervals of time:
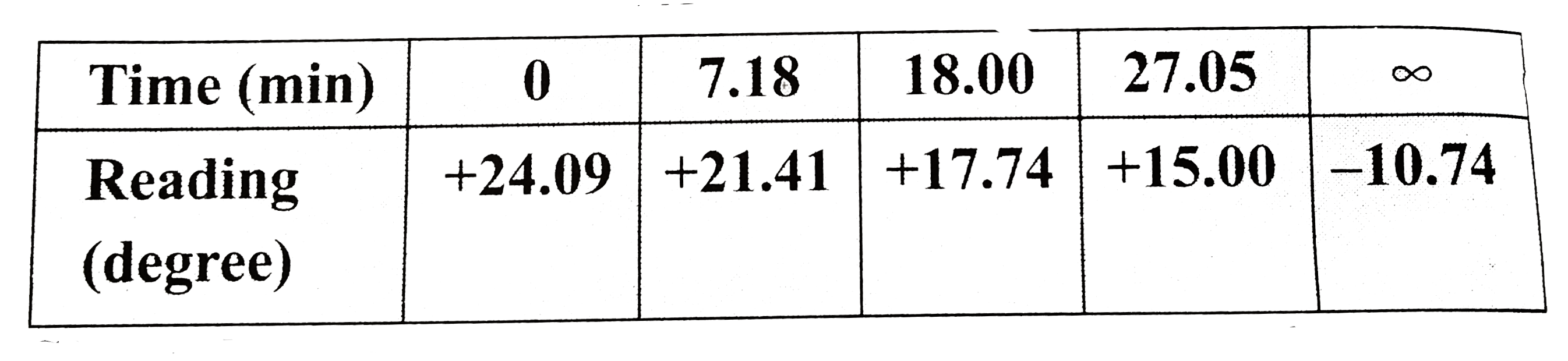
Show that the inverison of cane sugar is a unimolecular reaction.
View SolutionAt 373 K, the half-life period for the thermal decomposition of `"N"_(2)"O"_(5)` is 4.6 sec and is independent of the initial pressure of `"N"_(2)"O"_(5)`. Calculate the specific rate constant at this temperature.
View SolutionA first order reaction is found to have a rate constant, `k=5.5xx10^(-14)s^(-1)`. Find the half-life of the reaction.
View SolutionA first order reaction is `40%` complete in 50 minutes. Calculate the value of the rate constant. In what time will the reaction be `80%` complete?
View SolutionShow that in case of a first order reaction, the time required for `99.9%` of the reaction to take place is about `10` times that the required for half the reaction.
View SolutionThe reaction `SO_(2)Cl_(2) overset(k_(1))rarr SO_(2)+Cl_(2)` is a first order reaction with `k_(1) = 2.2 xx 10^(-5) s^(-1)` at `575 K`. What percentage of `SO_(2)Cl_(2)` will get decomposed in `90 min` when the reaction is carried out at `575 K`.
View SolutionThe initial concentration of `N_2O_5` in the first order reaction `N_2O_5 to 2NO_2 + 1//2O_2` was `1.24 xx10^(-2) "mol L"^(-1)` at 318 K. The concentration of `N_2O_5` after 60 minutes was `0.20 xx 10^(-2) "mol L"^(-1)`. Calculate the rate constant of the reaction at 318 K.
View SolutionA first order reaction has a specific reaction rate of `10^(-3)" sec"^(-1)`. How much time will it take for 10 g of the reactant to reduce to 2.5 g ? Given `log2=0.301, log4=0.6021,log6=0.778`.
View SolutionThe decomposition of `"N"_(2)"O"_(5)(g), i.e.,"N"_(2)"O"_(5)(g)to4"NO"_(2)(g)+"O"_(2)(g)` is a first order reaction with a rate constant of `5xx10^(-4)"sec"^(-1)" at "45^(@)C`. If intial concentration of `"N"_(2)"O"_(5)` is 0.25 M, calculate its concentration after 2 min. Also calculate half life for the decomposition of `"N"_(2)"O"_(5)(g).`
View SolutionThe rate constant for an isomerisation reaction `Ato B` is `4.5 xx 10^(-3)min^(-1)`. If the initial concentration of A is 1M, Calculate the rate of the reaction after 1 hour.
View SolutionThe following data were obtained the first order thermal decomposition of `"N"_(2)"O"_(5)(g)` at constant volume : `2"N"_(2)"O"_(5)(g)to2"N"_(2)"O"_(4)(g)+"O"_(2)(g)`
`{:("S. No.",,,"Time/s",,,"Total pressure (atm)"),(1,,,0,,,0.5),(2,,,100,,,0.512):}`
Calculate the rate constant.
View SolutionAT 373 K, a gaseous reaction A `rarr` 2B + C is found to be of first order. Starting with pure A, the total pressure at the end of 10 min. was 176 mm and after a long time when A was completely dissociated, it was 270 mm. The pressure of A at the end of 10 minutes was :
View SolutionThe decomposition of `Cl_(2)O_(7)` at 400 K in the gas phase to `Cl_(2)`
and `O_(2)` is a first order reaction.
(i) After 50 seconds at 400 K, the pressure of `Cl_(2)O_(7)` falls
from 0.062 to 0.044 atm. Calculate the rate constant.
(ii) Calculate the pressure of `Cl_(2)O_(7)` after 100 sec of
decomposition at this temperature.
View SolutionThe rate of a first order reaction is 0.04 mol `"litre"^(-1)s^(-1)` after 10 minutes and 0.03 mol `"litre"^(-1)s^(-1)` after 20 minutes. Find the half life period of the reaction.
View SolutionOne-fourth of a first order reaction is completed in 32 minutes. What is the half-life period of this reaction?
View SolutionAfter 24 hours, only 0.125 g out of the initial quantity of 1 g of a radioactive isotope remains behind. What is its half-life period ?
View SolutionHalf-life period of a radioactive element is 100 seconds. Calculate the disintegration constant and average life. How much time will it take to lose its activity by `90%`?
View SolutionThe rate constant of a reaction is `1.2xx10^(-3)sec^(-1)" at "30^(@)C" and "2.1xx10^(-3)sec^(-1)" at" 40^(@)C`.
Calculate the energy of activation of the reaction.
View SolutionThe rate of a particular reaction doubles when temperature changes from `27^(@)` C to `37^(@)C`. Calculate the energy of activation of such a reaction.
View SolutionThe activation energy of a reaction is 94.14 KJ/mol and the value of rate constant at `40^@ C` is `1.8 xx 10^(-1) sec^(-1)`. Calculate the frequency factor A.
View SolutionThe first order rate constant for the decompoistion of `C_(2)H_(5)I` by the reaction.
`C_(2)H_(5)I(g)rarrC_(2)H_(4)(g)+HI(g)`
at `600 K is 1.60xx10^(-5)s^(-1)`. Its energy of activation is `209 kJ mol^(-1)`. Calculate the rate constant at `700 K`
View SolutionRate constant k of a reaction varies with temperature according to the equation
`logk=" constant"-(E_(a))/(2.303).(1)/(T)`
where `E_(a)` is the energy of activation for the reaction. When a graph is plotted for log k versus `1//T`, a straight line with a slope -6670 K is obtained. Calculate the energy of activation for this reaction. State the units `(R=8.314" JK"^(-1)mol^(-1))`
View SolutionThe rate constant of a reaction of a reaction increases by `5%`
when the temperature of the reaction is increased
from 300 to 301 K where equilibrium constant increases
only by `2%`. Calculate the activation energy for the
forward as well as backward reaction.
View SolutionAt `27^(@)C` in the presence of a catalyst, the activation
?energy of a reaction is lowered by 2 kcal. Calculate
by how much the rate of reaction will increase ?
View SolutionA hydrogenation reaction is carried out at 500 K. If the same reaction is carried out in the presence of a catalyst at the same rate, the temperature required is 400 K. Calculate the activation energy of the reaction if the catalyst lowers the activation energy by 20 kJ `mol^(-1)` .
View SolutionThe rate constants of a reaction at 500 K and 700 K are `0.02s^(-1)` and `0.07s^(-1)` respectively. Calculate the values of `E_(a)` and A.
View Solution
PROBLEM questions and complete solutions for chapter CHEMICAL KINETICS of PRADEEP CHEMISTRY (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 CHEMISTRY CHEMICAL KINETICS
- ADDITIONAL QUESTIONS (LONG ANSWER QUESTIONS)
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) I. General introduction and rates of reactions
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) II. Rate law, order of reaction, rate constant and its units
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) III. Molecularity, mechanism and difference between order and molecularity
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) IV. Integrated rate equations, half-life, determination of rate law, rate const, and order
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) V. First order reactions, pseudo first order reactions and reactions and radioactive disintegration
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) VI. Activation energy, effect of temp. on rate (Arrhenius eqn.) and effect of catalyst on rate
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) VII. Collision theory
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) VIII. Miscellaneous
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) I. General introduction and rates of reactions
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) II. Rate law, order of reaction, rate constant and its units
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) III. Molecularity, mechanism and difference between order and molecularity
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) IV. Integrated rate equations, half-life, determination of rate law, rate const. and order
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) V. First order reactions, pseudo first order reactions and radioactive disintegration
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) VI. Activation energy, effect of temp. on rate (Arrhenius eqn.) and effect of catalyst on rate
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS) VII. Collision theory
- ADVANCED PROBLEMS FOR COMPETITIONS
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VI. Integer Type Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VII. Assertion-Reason Type Questions) Type - I
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VII. Assertion-Reason Type Questions) Type - II
- COMPETITION FOCUS (IV. Matching Type Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (IV. Matching Type Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (V. Matrix-Match Type Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (I. Multiple Choice Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (I. Multiple Choice Questions) (III. Multiple Choice Questions) Based on Comprehension
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (I. Multiple Choice Questions) With one or more than one correct answers
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (II. Multiple Choice Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VI. Integer Type Questions)
- COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VIII. Multiple Choice Questions)
- COMPETITION FOCUS (V. Matrix-Match Type Questions)
- CONCEPTUAL QUESTIONS (I. General introduction and rates of reactions)
- CONCEPTUAL QUESTIONS (II. Rate law, order of reaction, rate constant and its units)
- CONCEPTUAL QUESTIONS (III. Molecularity of a reaction, its mechanism and difference between order and molecularity)
- CONCEPTUAL QUESTIONS (IV. Integrated rate equations, half-life, determination of rate law, rate constant and order)
- CONCEPTUAL QUESTIONS (V. First order reactions, pseudo first order reactions and radioactive disintegration)
- CONCEPTUAL QUESTIONS (VI. Activation energy, effect of temp. on rate (Arrhenius eqn.) and effect of catalyst on rate)
- CONCEPTUAL QUESTIONS (VII. Collision theory)
- CURIOSITY QUESTION
- HIGHER ORDER THINKING SKILLS (QUESTIONS AND PROBLEMS WITH ANSWERS/SOLUTIONS) HOTS PROBLEMS
- HIGHER ORDER THINKING SKILLS (QUESTIONS AND PROBLEMS WITH ANSWERS/SOLUTIONS) HOTS QUESTIONS
- IMPORTANT QUESTIONS FOR BOARD EXAMINATION
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (ASSERTION AND REASON TYPE OUESTIONS)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (ASSERTION AND REASON TYPE QUESTIONS)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (LONG ANSWER QUESTIONS)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (MATCHING TYPE QUESTIONS)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (MULTIPLE CHOICE QUESTIONS-1)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (MULTIPLE CHOICE QUESTIONS-II)
- NCERT EXEMPLAR PROBLEMS WITH ANSWERS, HINTS AND SOLUTTIONS (SHORT ANSWER QUESTIONS)
- NCERT EXERCISES
- NCERT QUESTIONS AND EXERCISES WITH ANSWERS (NCERT INTEXT UNSOLVED QUESTIONS & PROBLEMS)
- PROBLEM
- PROBLEMS FOR PRACTICE
- TEST YOUR GRIP (FILL IN THE BLANK)
- TEST YOUR GRIP (MULTIPLE CHOICE QUESTIONS)
- VALUE BASED QUESTIONS (WITH ANSWERS)