वास्तविक संख्या कक्षा 10 गणित
भूमिका
सभी परिमेय व अपरिमेय संख्याओ का संग्रह वास्तविक संख्यायें कहलाता है, जिसमे धनात्मक, ऋणात्मक तथा शून्य सभी प्रकार की संख्यायें सम्मिलित है। इस अध्याय में हम पूर्णांकों की भाजकता तथा परिमेय-अपरिमेय संख्याओं के गुणों का अध्ययन करेंगे।
वास्तविक संख्याएँ
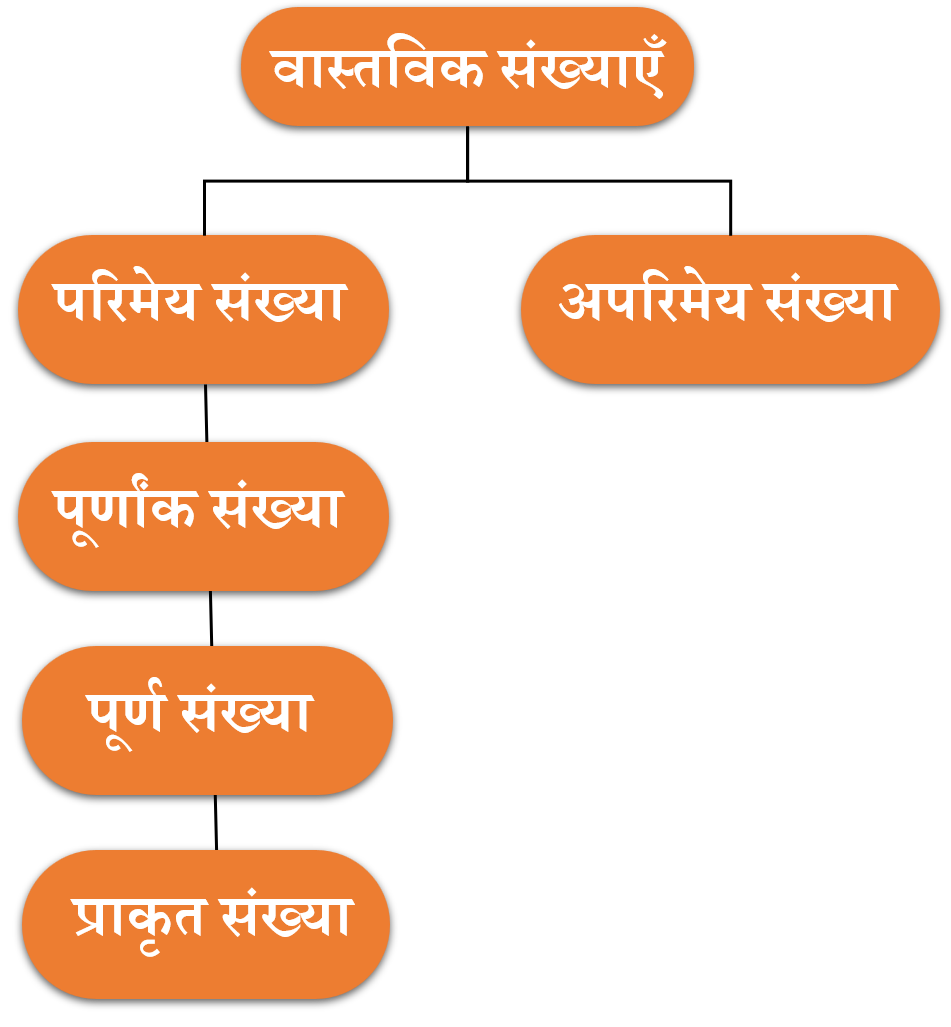
- सभी परिमेय और अपरिमेय संख्याओं का संग्रह वास्तविक संख्याएँ कहलाता है।
- वास्तविक संख्याएँ पूर्णांक, भिन्नात्मक तथा दशमलव संख्याये होती हैं।
- वास्तविक संख्याओं में शून्य के साथ सभी धनात्मक और ऋणात्मक संख्याएँ सम्मिलित होती हैं।
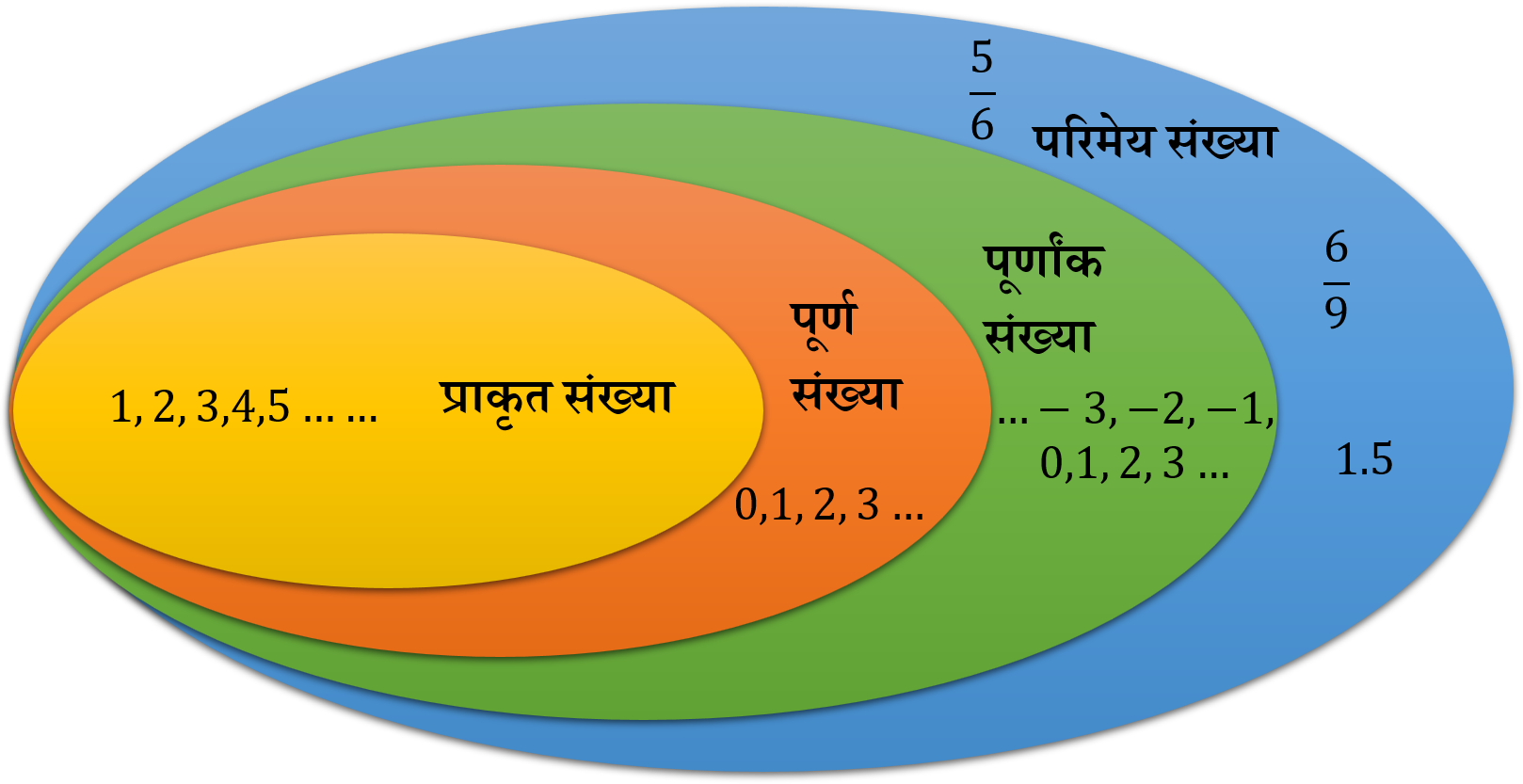
NOTE: परिमेय संख्या में सभी प्राकृत, पूर्ण तथा पूर्णांक संख्याएँ सम्मिलित होती है।
1. प्राकृत संख्याएँ (N): 1, 2, 3, 4,..........
2. पूर्ण संख्याएँ (W): 0, 1, 2, 3, 4……….
3. पूर्णांक संख्याएँ ( Z या I): …….-2, -1, 0, 1, 2,......
4. परिमेय संख्याएँ (Q): −23, −1, 0, 2, 254…….
5.अपरिमेय संख्याएँ (Qc): √2, π, √32, 3√5, 2+√7.........
NOTE: π एक अपरिमेय संख्या है जबकि 227 एक परिमेय संख्या है।
यूक्लिड विभाजन प्रमेयिका
यूक्लिड विभाजन प्रमेयिका के अनुसार दो धनात्मक पूर्णांक a और b दिए रहने पर, ऐसी अद्वितीय पूर्ण संख्याएँ (अऋणात्मक पूर्णांक) q और r विद्यमान हैं कि a=b×q+r जहाँ 0≤r<b है।
यूक्लिड विभाजन एल्गोरिथ्म
यूक्लिड विभाजन एल्गोरिथ्म दो धनात्मक पूर्णांकों का HCF परिकलित करने की एक तकनीक है।
दो धनात्मक पूर्णांकों, मान लीजिए a और b (a>b) का HCF ज्ञात करने के लिए नीचे दिए गए चरणों का अनुसरण कीजिएः
चरण 1 : a और b के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए। यहाँ हम ऐसे q और r ज्ञात करते हैं कि a=bq+r,0≤r<b हो।
चरण 2 : यदि r=0 है, तो b पूर्णांकों a और b का HCF है। यदि r≠0 है, तो b और r के लिए यूक्लिड विभाजन प्रमेयिका का प्रयोग कीजिए।
चरण 3 : इस प्रक्रिया को तब तक जारी रखिए, जब तक शेषफल 0 न प्राप्त हो जाए। इसी स्थिति में, प्राप्त भाजक ही वांछित HCF है।
यह एल्गोरिथ्म इसलिए प्रभावशाली है, क्योंकि HCF(a,b)=HCF(b,r) होता है, जहाँ संकेत HCF (a, b ) का अर्थ है a और b का HCF।
स्मरणीय तथ्य
- प्रमेयिका एक सिद्ध किया हुआ कथन होता है, इसे किसी अन्य कथन को सिद्ध करने के लिए प्रयोग किया जाता है।
- एल्गोरिथ्म सुपरिभाषित चरणों की एक श्रृंखला होती है, जो एक विशेष प्रकार की समस्या को हल करने की एक प्रक्रिया या विधि प्रदान करती है।
अंकगणित के आधारभूत प्रमेय
प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के धनात्मक घातों के एक गुणनफल के रूप में व्यक्त (गुणनखंडित) किया जा सकता है तथा यह गुणनखंडन अद्वितीय होता है।
स्मरणीय तथ्य
- वे 1 से बड़ी प्राकृतिक संख्याएँ, जो स्वयं और 1 के अतिरिक्त और किसी प्राकृतिक संख्या से विभाजित नहीं होतीं, उन्हें अभाज्य संख्या कहते हैं।
- वे 1 से बड़ी प्राकृतिक संख्याएँ जो अभाज्य संख्या नहीं हैं, उन्हें भाज्य संख्या कहते है।
- दो या दो से अधिक संख्याओं के बीच यदि अधिकतम उभयनिष्ठ गुणनखंड "1" हो तो वे संख्याएँ सहअभाज्य संख्याएँ कहलाती है।
जैसे की 4(=2x2x1) व 3(=3x1) के मध्य केवल 1 उभयनिष्ट है, अतः यह दोनों संख्याएँ अर्थात 4 और 3 सहअभाज्य होंगी।
- किसी भाज्य संख्या के अद्वितीय अभाज्य गुणनखंड प्राप्त होते है।
20=2×2×5×1 यहाँ 20 के गुणनखंड अद्वितीय है अर्थात इसके अलावा अन्य कोई अभाज्य गुणनखंड प्राप्त करना संभव नहीं है।
- दो लगातार संख्याओ का HCF 1 होता है क्योंकि उनके अभाज्य गुणनखंड में 1 ही उभयनिष्ट होता हैं।
- दो लगातार संख्याओ का LCM उन संख्याओ का गुणनफल होता हैं।
- HCF(a,b)×LCM(a,b)=a×b
- HCF(a,b,c)×LCM(a,b,c)≠a×b×c
परिमेय व अपरिमेय सँख्याएँ
परिमेय संख्या (Rational Numbers) :
एक परिमेय संख्या pq, (q≠0 तथा p,q∈Z(पूर्णांक)) को परिमेय संख्या का मानक रूप कहा जाता है। यदि p,q में 1 को छोड़कर कोई दूसरा उभयनिष्ठ गुणनखण्ड नहीं हो अर्थात H.C.F(p,q)=1
अपरिमेय संख्या (Irrational Numbers):
कोई भी संख्या जो pq जहाँ p और q पूर्णाक हैं और q≠0, के रूप में नहीं लिखा जा सके, अपरिमेय संख्या कहलाती है।
NOTE: √2,√3 इत्यादि अपरिमेय संख्यायें हैं अर्थात √a (√PrimeNumbers) एक अपरिमेय संख्या है जहाँ a एक अभाज्य संख्या है।
√a = अपरिमेय संख्या, जहाँ a एक अभाज्य संख्या है।
√a = अपरिमेय संख्या सिद्ध करने के लिए विरोधोंक्ति विधि का प्रयोग किया जाता है।यहाँ सर्वप्रथम विपरीत कथन (माना, √2 = परिमेय संख्या) मान कर हल करना है तथा अंततः लिए गए कथन को गलत (√2≠ परिमेय संख्या) सिद्ध करके उचित कथन (√2 = अपरिमेय संख्या) प्राप्त करेंगे। (NCERT प्रमेय 1.4)
दशमलव प्रसार के आधार पर जांच
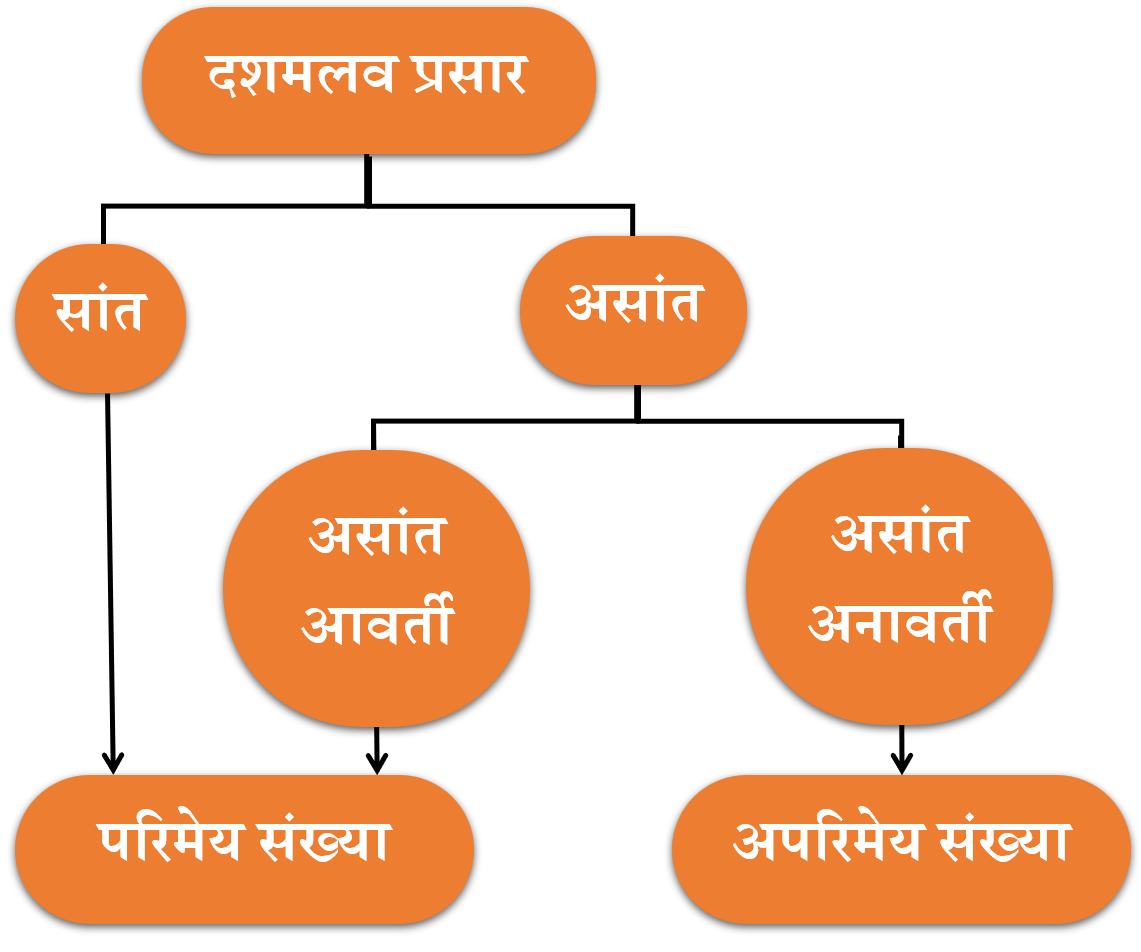
बिना लंबी विभाजन प्रक्रिया के जांच करना
यदि कोई परिमेय संख्या (pq) ज्ञात है जहां p व q सहअभाज्य संख्या है तब हर अर्थात q के आधार पर परिमेय संख्या का दशमलव प्रसार सांत या असांत आवर्ती ज्ञात किया जा सकता है।
सांत `=>` `q=2^n5^m`
मान लीजिए x एक ऐसी परिमेय संख्या है जिसका दशमलव प्रसार सांत है। तब x, को pq के रूप में व्यक्त किया जा सकता है, जहाँ p और q सहअभाज्य हैं तथा q का अभाज्य गुणनखंड 2n5m के रूप का है, जहाँ, m व n कोई ऋणेतर पूर्णांक (पूर्ण संख्याएँ 0, 1, 2...) हैं।
`q=2^n5^m``=>` सांत
मान लीजिए x=pq जहाँ p और q सहअभाज्य हैं, एक परिमेय संख्या ऐसी है कि q, 2n5m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक हैं। तब x का दशमलव प्रसार सांत होता है।
`q!=2^n5^m``=>` असांत आवर्ती
मान लीजिए x =pq, जहाँ p और q सहअभाज्य हैं, एक परिमेय संख्या इस प्रकार है कि q का अभाज्य गुणनखंडन 2n5m के रूप का नहीं है, जहाँ n, m ऋणेतर पूर्णांक हैं, तब x का दशमलव प्रसार असांत आवर्ती होता है।
NOTE: q=2n या 5m या 2n5m रूप प्राप्त हो सकता है, जहां n, m पूर्ण संख्याएँ (n,m =0,1,2...) है।
स्मरणीय तथ्य
- एक परिमेय संख्या और एक अपरिमेय संख्या का योग या अंतर एक अपरिमेय संख्या होती है।
- एक शून्येतर (शून्य के अतिरिक्त) परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल एक अपरिमेय संख्या होती है।
निम्न सारणी से समझो