A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
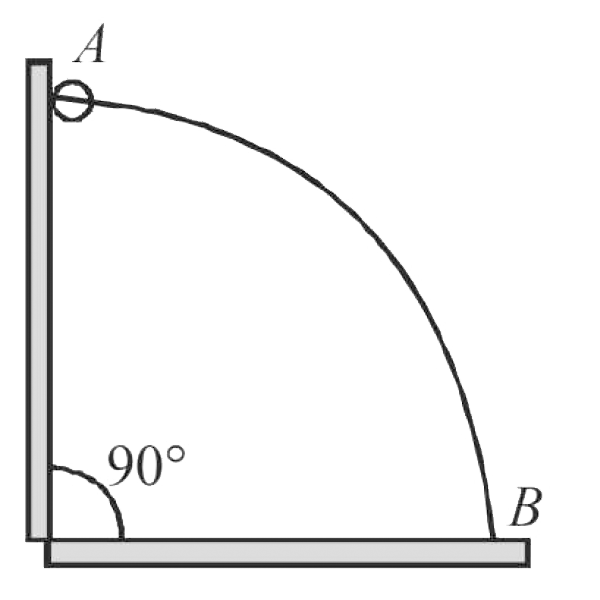
always radially outwards
always radially inwards
raidally outwards initially and inwards later
radially inwards initially and radially outwards later
The correct Answer is:D
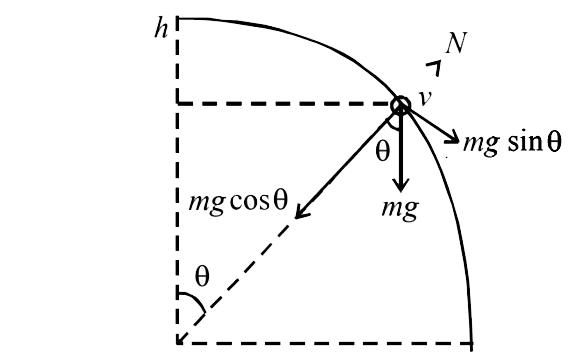
As the bead is moving in the circular path
∴ mgcosθ−N=mv2R
∴ N=mgcosθ−mv2R …(1)
By energy conservation, 12mv2=mg[R−Rcosθ]
∴ (v^2)/(R)=2g(1-costheta)...(2)<br>From(1)and(2)<br>N=mg cos theta-m[2g-2gcos theta]<br>N=mg cos theta-2mg+2mgcostheta<br>N=3mg cos theta-2mg<br>implies N=mg(3costheta-2)<br>C≤arlyNispositive(actsradiallyoutwards)whencosthetagt2/3<br>Similarly,Nactsradially∈wardsifcos thetalt2/3
Similar Questions
A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solutionएक तार जो एक छोटे मोती के मध्य में स्थित छिद्र से गुजरता है, को एक चतुर्थाशा वृत्त के अनुरूप मोड़ा गया है। तार को भूमि पर उर्ध्व तल में स्थित किया गया है, जैसा चित्र में दर्शाया गया है । मोती को तार के ऊपरी सिरे से छोड़ा जाता है, जिससे यह तार के अनुदिश, बिना किसी घर्षण के सरकता है। जब मोती A से B तक सरकता है। तब इसके द्वारा तार पर लगने वाला बल है:

View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionA frictionless wire is fixed between A and B inside a circle of radius R . A small bead slips along the wire. Find the time taken by the bead to slip from A to B .
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x^(2) =4ay . The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
View Solution

