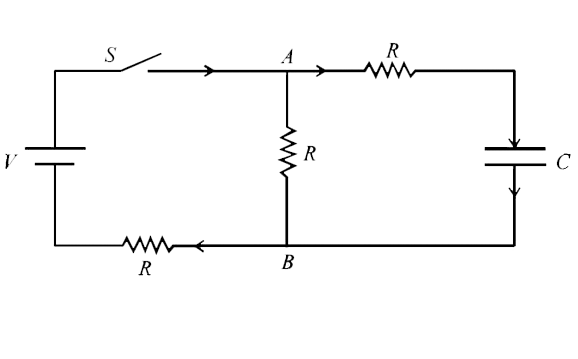
In the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
 .
.
The correct Answer is:A, B, C
Let at any time t charge on capacitor C be Q. Let currents are
as shown in fig. Since charge Q will increase with time 't'
therefore i1=dQdt
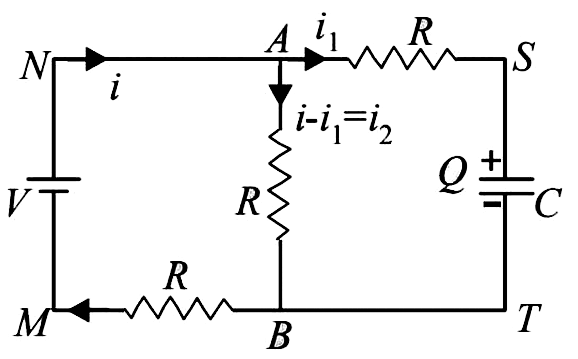
(a) Applying Kirchoff's second law in the loop MNABM.
V=(i−i1)R+iR
or V=2iR−i1R..........(i)
Similarly, applying Kirchoff's second law in loop MNSTM,
we have
V=i1R+QC+iR ......(ii)
Eliminating i from equation (1) and (2), we get
V=3i1R+2QCor3i1R=V−(2QC)
or i1=13R(V−2QC)ordQdt=13R(V−2QC)
or dQV−2QC=dt3Ror∫Q0dQV−2QC=∫t0dt3R
This equation gives Q =CV2(1−e−2t/3RC)
(b) i1=dQdt
i1=ddt[CV2(1−e−2t/3RC)]
=CV2×23RC×e−2t3RC=V3Re−2t/3RC
From equation(i)
i=V+i1R2R=V+V3e−2t/3RC2R
∴CurrentthroughAB
i2=i−i1=V+V3e−2t/3RC2R - V/R e^(-2t//3RC)<br>i_2 = V/(2R) - V/(6R) e^(-2t//3RC)<br>i_2 = V/(2R) as t rarr oo .
Similar Questions
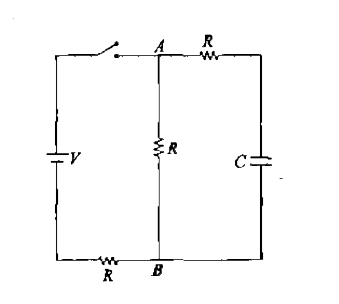
In the circuit shown in figure-3.244, the battery is an ideal one with emf V. The capacitor is initially uncharged. The switch S is closed at time t=0.
(a) Find the charge Q on the capacitor at time l
(b) Find the current in branch AB at time just after closing the switch.
View SolutionIn the circnit shown, capacitor is initially uncharged till the switch is turned on at time t=0. Then

View Solution
Knowledge Check
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
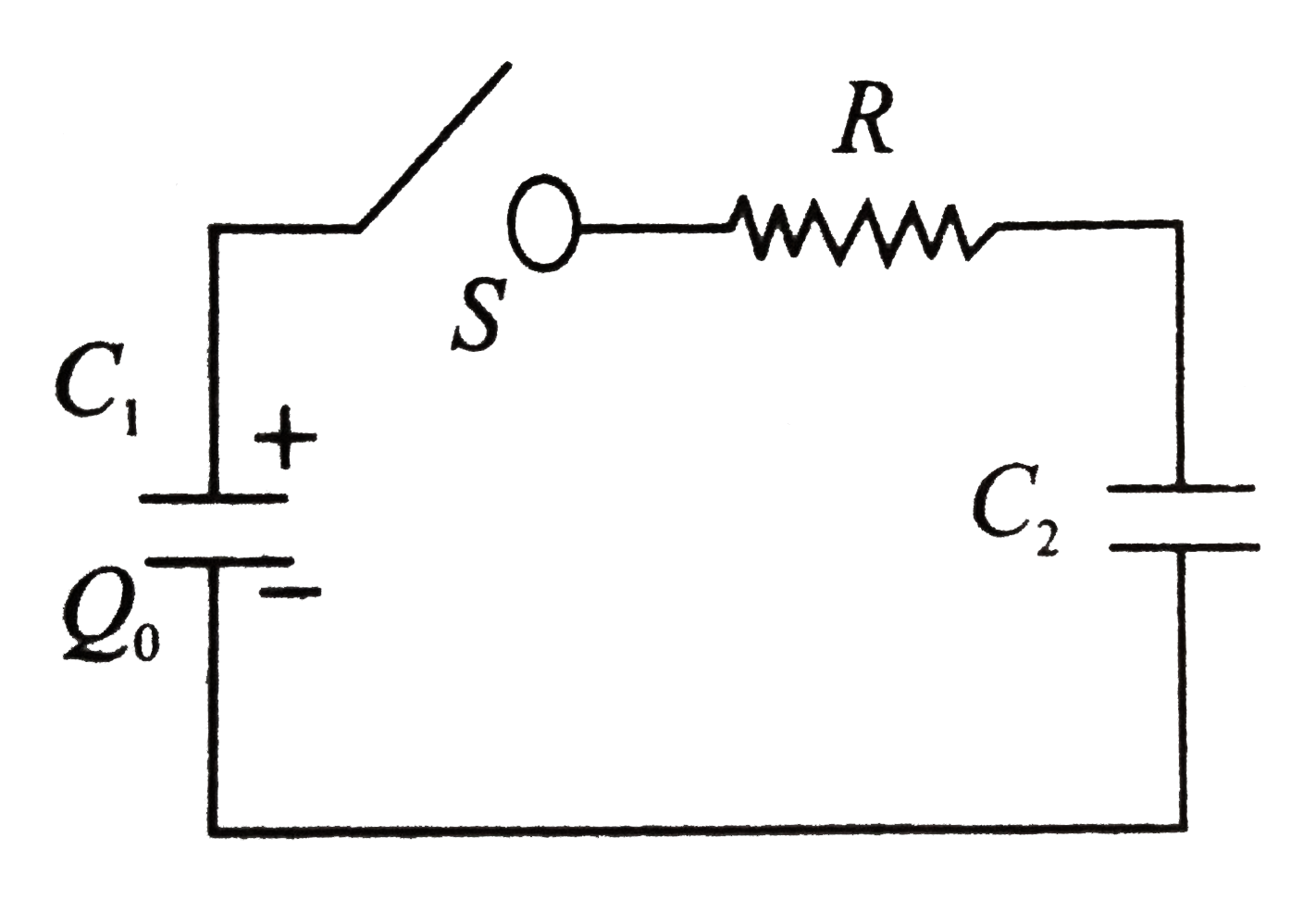 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)In the circuit shown, the capacitor is initially uncharged. The switch S is closed at t = 0. Time after which voltage across capacitor and resistor are equal is:
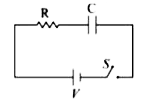 ARCln12BRCln2CRCln32DRC
ARCln12BRCln2CRCln32DRCThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
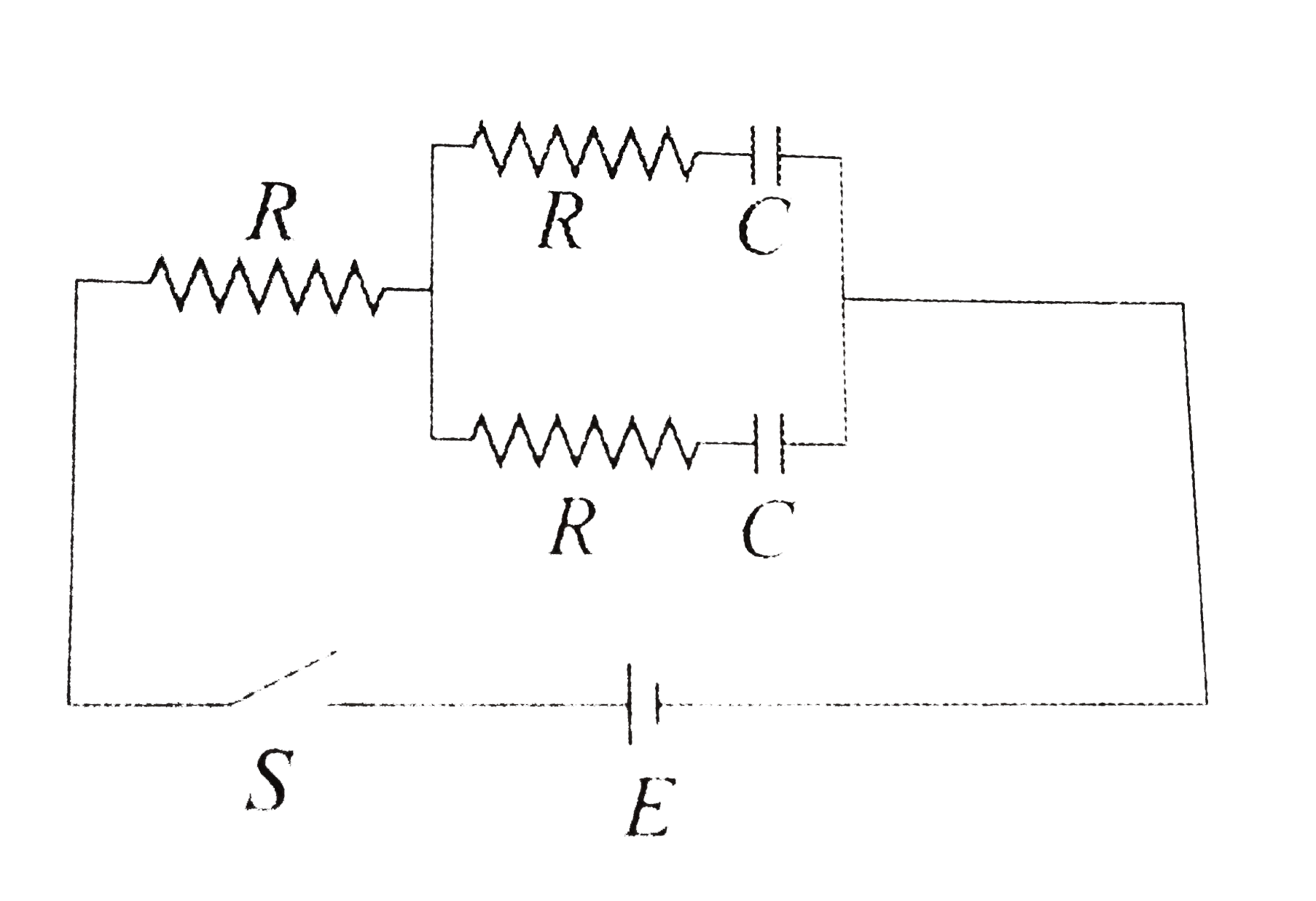 Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
Aqt=EC(1−e−2t/3RC)Bqt=EC(1−e−t/2RC)Cqt=EC(1−e−t/3RC)Dqt=EC(1−e−3t/2RC)
In the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
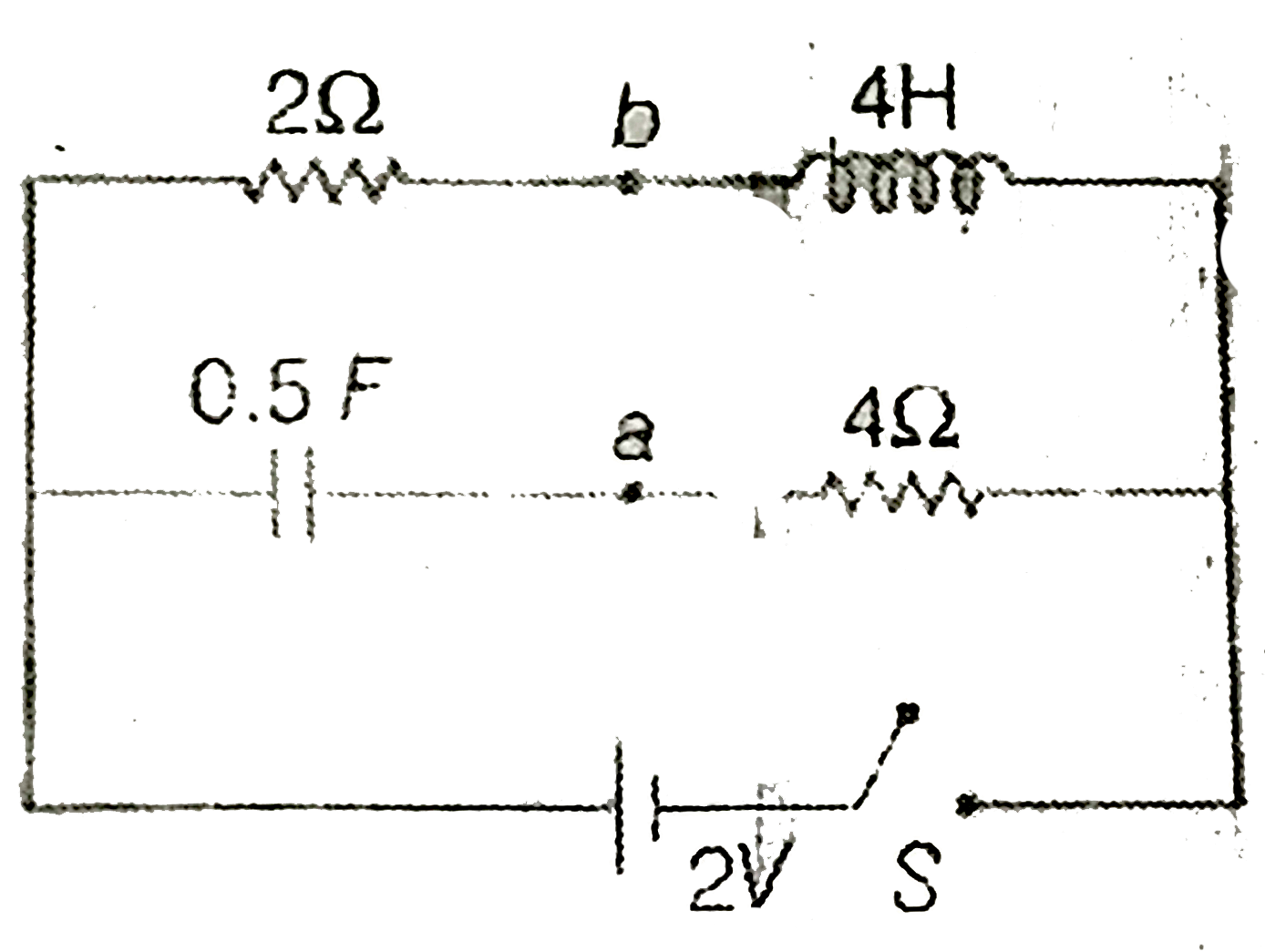
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
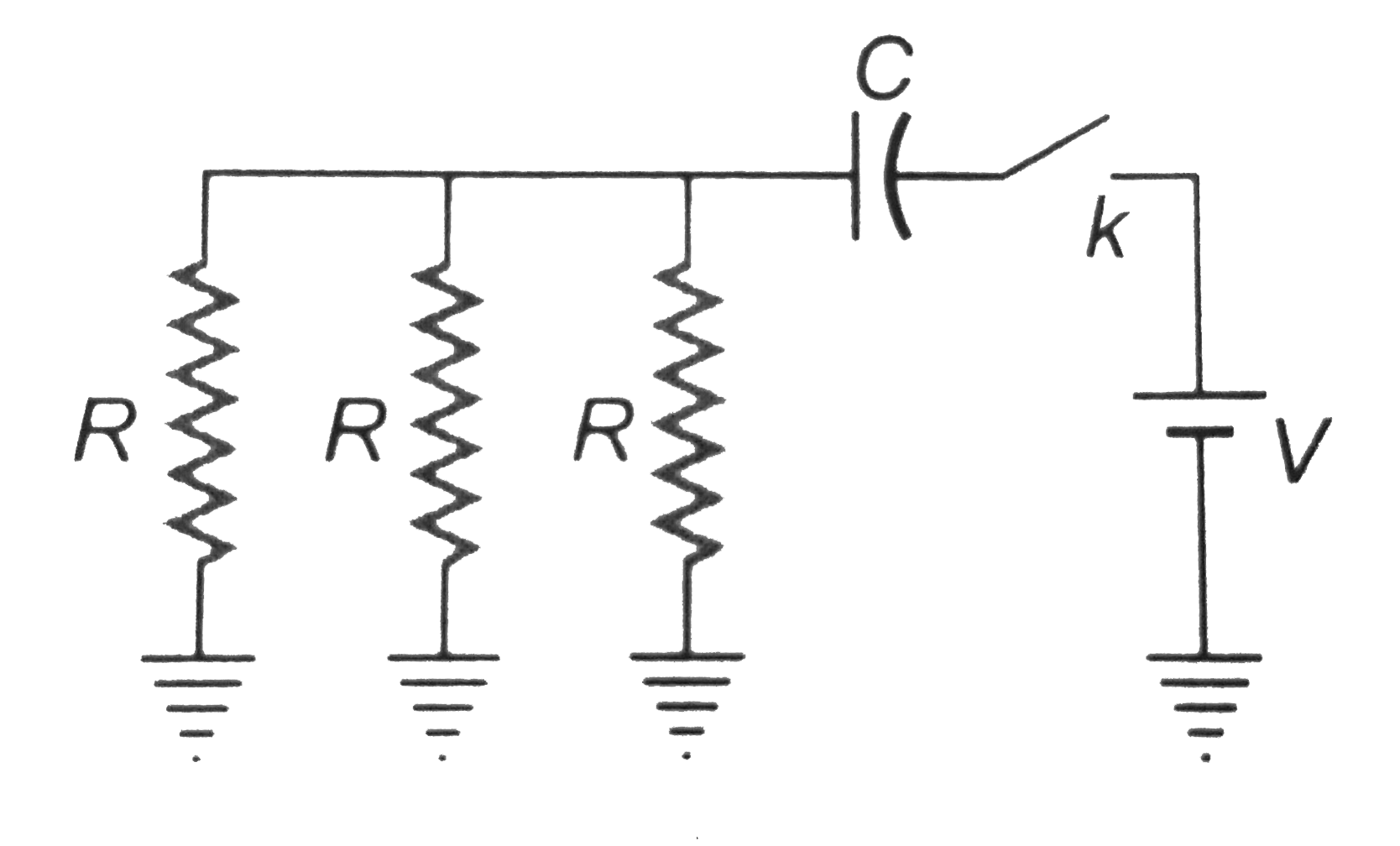
View Solution
