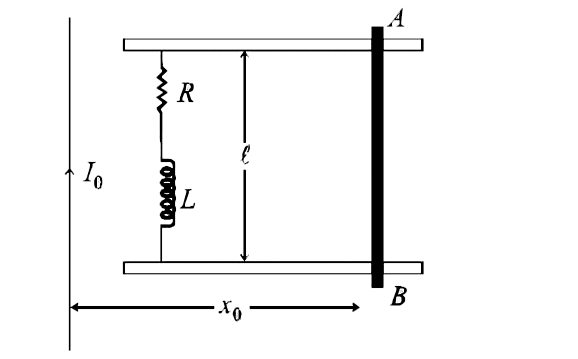
A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
The correct Answer is:A, B, C, D
As the metal bar AB moves towards the right the magnetic flux in the loop. ABCD increases in the downward direction. By Lenz's law, to oppose this current will flow inanticlock wise direction as shown in figure.
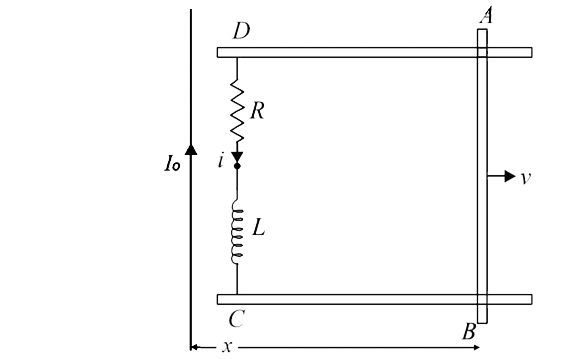 Applying Kirchhoff's loop law in ABCD, we get
Applying Kirchhoff's loop law in ABCD, we get
dϕdt=iR+Ldidt( ...(i)(b) Let AB beat a distance x fro the long striaght wire at any instant of time t during its mition, The magnetic field at that instant at AB due to lang striaght current carrying wire is
B=μ0I02πx)
The change in flux through ABCD in time dt is
(dϕ)=B(dA)=Bldx
Therefore, the total flux change when metal bar moves from a distance (x0)→2(x0) is
(Δϕ)=∫2x0x0Bldx=l∫2x0x0μ0I02πdx=μ0I0l2π[logex]2x0x0
=μ0I0l2πloge2 ....(ii) THe charge flowing through resistance R in time T is
q=∫T0∫T0[E∈duced−Ldidt]dt(omeq.(i))<br>=1/R int_(0)^(T) E_(induced) dt -L/R int _(0)^(l_1) d i=1/R (Delta phi)-L/R(i_1)<br>q=1R[μ0I0l2πloge2]−LR(i1)omeq(ii)
(c) When the metal bar AB is stopped, the rate of change of magnetic flu through ABCD bexomes zero. from (i),
iR=−Ldidt
∫2TTdt=LR∫i1/4i1dii
T==-L/R log_(e) (i_(1)//4)/(i_1) implies L/R=T/(2 log_(e)2).
Similar Questions
A copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
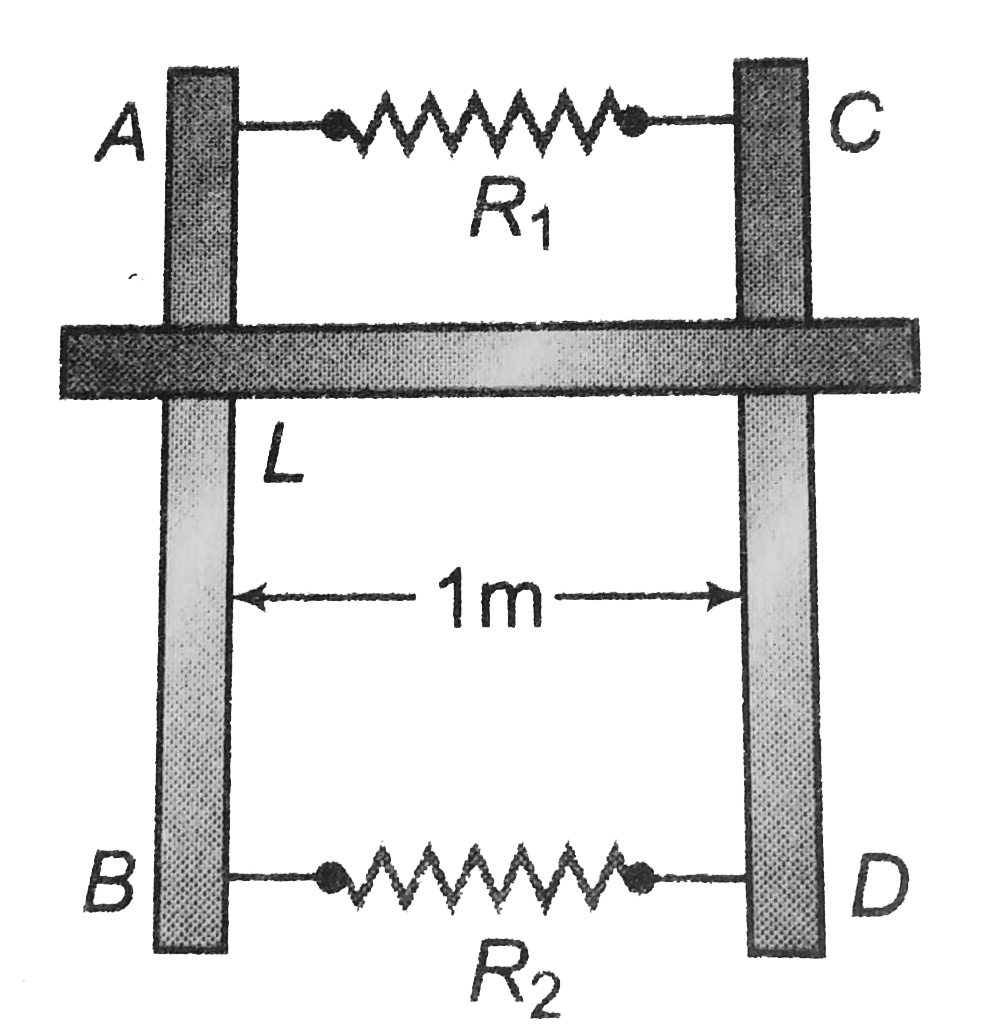
The terminal velocity fo the bar L will be
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.

View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
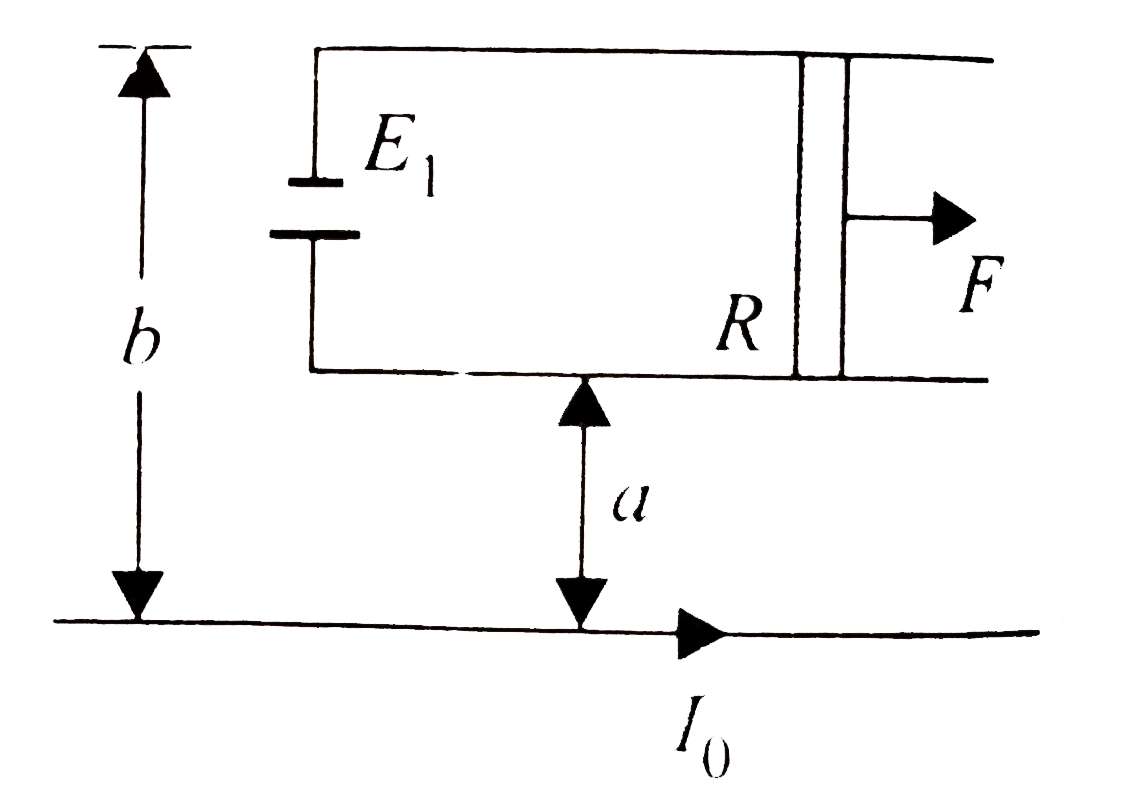
Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
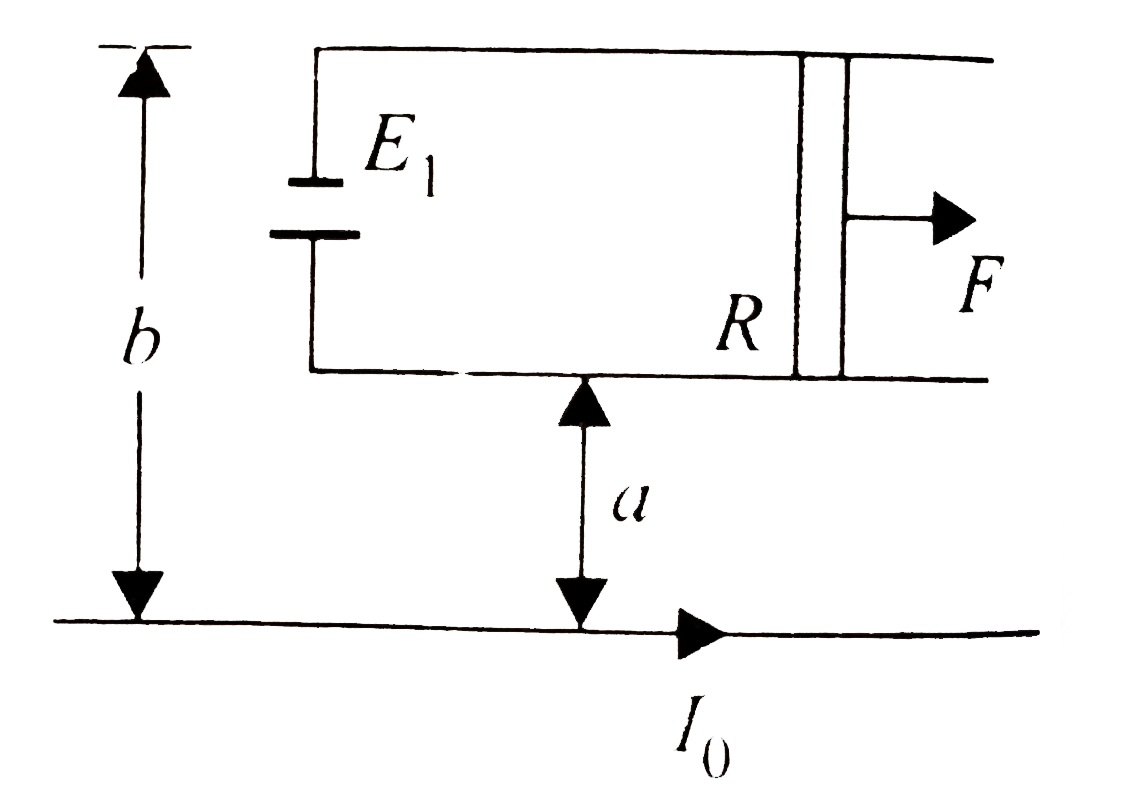
Find the value of F if the rod slides with constant velocity
View Solution
