निम्नलिखित फलन का उच्चतम और न्यूनतम मान ज्ञात करें:
x2−7x+6x−10
Video Solution
Text Solution
माना की y=x2−7x+6x−10
∴dydx=(x−10)(2x−7)−(x2−7x+6)⋅1(x−10)2 ....(1)
2x2−27x+70−x2+7x−6(x−10)2=x2−20x+64(x−10)2 ...(2)
चूँकि (x−10)2>0, इसलिए dydx के लिए चिन्ह योजना भी होगा जो x2−20x+64
के लिए
अब, x2−20x+64=0⇒x=4,16
dydx अर्थात x2−20x+64 के लिए योजना
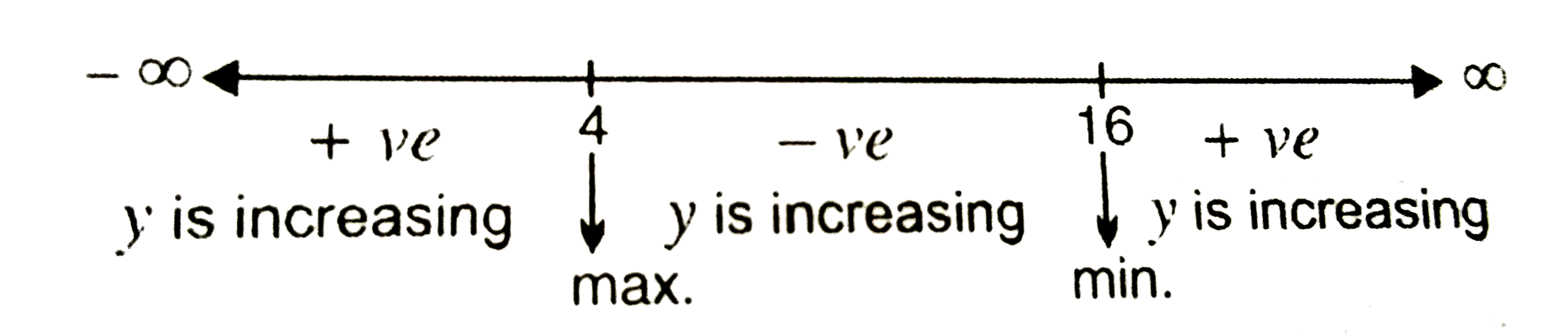
y का मान x =4 पर महत्तम है|
(1) से y संगत महत्तम मान =42−7×4+64−10=1
y का मान x =16 न्यूनतम है|
(1) से y संगत न्यूनतम मान =162−7×16+616−10=1506=25
दूसरी विधि
माना की y=x2−7x+6x−10
∴ dydx=x2−20x+64(x−10)2
y के महत्तम और न्यूनतम मान के लिए dydx=0
∴ x2−20x+64=0⇒x=4,16
(2 ) से dydx=x2−20x+100−100+64(x−10)2
=(x−10)2−36(x−10)2=1−36(x−10)2 ...(3)
∴d2ydx2=72(x−10)3 ...(4)
x =4 पर, d2ydx2=72(−6)=−13<0
अतः y का मान x =4 पर महत्तम है|
x =16 पर, d2ydx2=7263=13>0
अतः y का मान x =16 पर न्यूनतम है|
(1 ) से,y का संगत न्यूनतम मान =25
|
Similar Questions
1+cosec2x का न्यूनतम मान ज्ञात कीजिए।
View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=−(x−1)2+10
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionफलन logxx का, अन्तराल [2,∞) में न्यूनतम मान होगा
View Solutionकिसी संवृत अंतराल में किसी फलन का उच्चतम एवं निम्नतम मान ज्ञात करना | उदाहरण
View Solutionअवकलन |फलन का उच्चतम तथा निम्नतम मान |प्रश्न |OMR|Summary
View SolutionFind the value of/ निम्नलिखित का मान ज्ञात करें: (3576+4286+6593)÷(201+105+107) is :-
View Solution
