यदि f:R→R,f(x)=x3+1 से परभाषित है और g:R→R.
g(x)=x+1 से परिभाषित है तो ज्ञात कीजिए f+g,f−g,f⋅g,fg और αf(α∈R)
वीडियो समाधान
लिखित उत्तर
f+g:R→R में परिभाषित है ।
अब (f+g)(x)=f(x)+g(x)=x3+1+x+1=x3+x+2
f−g:R→R में परिभाषित है ।
(f−g)(x)=f(x)−g(x)=x3+1−x−1=x3−x
f⋅g:R→R में परिभाषित है ।
(fg)(x)=f(x)g(x)=(x3+1)(x+1)=x4+x3+x+1
fg:R−{−1)→R में परिभाषित है ।
(fg)(x)=f(x)g(x)=x3+1x+1=(x+1)(x2−x+1)x+1=x2−x+1
αf:R→R में परिभाषित है ।
(αf)(x)=αf(x)=α(x3+1)=αx3+α
|
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
limx→0n√1−x−1x=
View Solutionयदि f:R→R,f(x)=2x+1 और g:R→R,g(x)=x3, तो (gof)−1(27) बराबर है
View Solutionमाना R वास्तविक संख्याओं का समुच्चय है और फलनों f:R→R और g:R→R द्वारा दर्शाया गया है। यदि f(x)=x2+2x−3 और g(x)=x+2 , तब x का मान क्या है? यदि f(g(x))=g(f(x)) है:
View SolutionIf f:R→R and g:R→R are given by f(x)=|X| and g(x)=[x] for each x∈R then {x∈R:g(f(x))≤f(g(x))} is equal to
View SolutionIf f:R→R and g:R→R are defined by f(x)=x−[x] and g(x)=[x]∀x∈R,f(g(x))=
View SolutionIf f:R→R and g:R→R are given by f(x)=|x| and g(x)=[x] for each x∈R, then {x∈R:g(f(x))≤f(g(x))}=
View SolutionIf f:R→R,f(x)=x−2,g:R→R,g(x)=x+2 then (f+g)(x)= ……..
View SolutionA table of values of f, g, f' and g' is given:
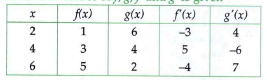 . If R(x) = g[3+ f(x)] , find r'(4)
. If R(x) = g[3+ f(x)] , find r'(4)
View Solution

