बहुपद 3x2+2x−1=0 को हल कीजिए ।
वीडियो समाधान
लिखित उत्तर
माना y=f(x) अथवा y=−3x2+2x−1
x के विभिन्न मानो के लिए y के मान नीचे दी गयी सारणी में अंकित है |
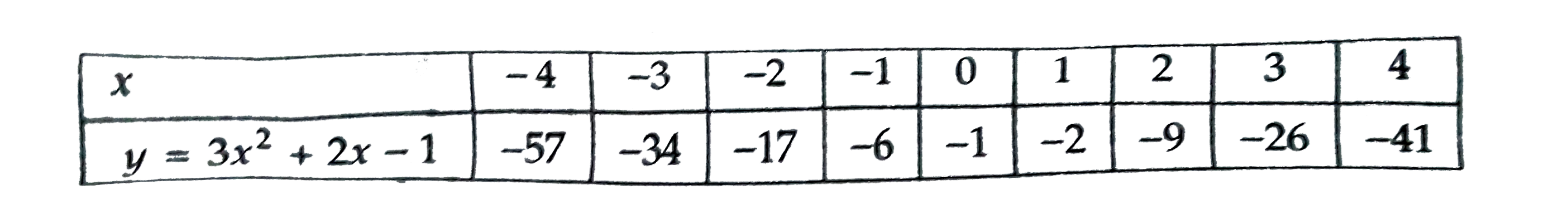
अतः y=−3x2+2x−1 का आलेख बिंदुओं (−4,−57),(−3,−34),(−2,−17),(−1,−6),(0,−1),(1,−2),(2,−9),(3,−26) और (4,−41) से होकर गुजरता है |
अब ग्राफ पेपर पर इन बिंदुओं को अंकित करके इनसे गुजरने वाला वक्र खींचते है | इस प्रकार प्राप्त वक्र चित्र में दर्शाया गया है |
प्रेक्षण : बहुपद f(x)=−3x2+2x−1 के आलेख से निम्न निष्कर्ष निकलते है |
(i) बहुपद f(x)=−3x2+2x−1 में x2 का गुणांक -3 , अर्थात ऋणात्मक वास्तविक संख्या है अतः परवलय नीचे की ओर खुलता है |
(ii) बहुपद f(x)=−3x2+2x−1 के गुणनखण्ड नहीं हो सकते है | अतः परवलय x - अक्ष को स्पर्श नहीं करता है और न ही x - अक्ष को काटता है |
(iii) बहुपद f(x)=−3x2+2x−1 के कोई वास्तविक शून्यक नहीं है इसलिए परवलय x - अक्ष को न तो स्पर्श करता है और न ही x - अक्ष को काटता है |
(iv) बहुपद f(x) के सभी मान ऋणात्मक है क्योंकि परवलय नीचे की ओर खुलता है और x - अक्ष के नीचे रहता है |
(v) बहुपद f(x)=−3x2+2x−1 की ax2+bx+c, से तुलना करने पर a=−3, और c=−1 पाते है | परवलय का शीर्ष (−b2a,−D4a) अर्थात (13,−23) है , जहाँ D=b2−4ac है |
|
समान प्रश्न
निम्नलिखित अवकलन समीकरणों को हल कीजिए-
dydx+3x−2y−52x+3y−5=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
(2x+y+1)dx+(4x+2y−1)dy=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
dydx=1−3x−3y2(x+y)
View Solutionनिम्न को हल कीजिए
∣∣x2+4x+3∣∣+2x+5=0
View Solutionनिम्नलिखित प्रत्येक समीकरण को हल कीजिए :
3+2x=6412+2713
View Solutionहल कीजिए तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
2x−3<5
View Solutionहल कीजिए तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
3−4x≤5
View Solutionहल कीजिए 3x−42≥x+14−4 तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
View Solution