बहुपद f(x)=3x4+6x3−2x2−10x−5 के सभी शून्यक ज्ञात कीजिये यदि इसके दो शून्यक √53 और −√53 है |
Video Solution
Text Solution
चूँकि √53 और −√53 बहुपद f(x) के दो शून्यक है |
∴(x−√53)(x+√53)=(x2−53)=13(3x2−5) बहुपद f(x) का गुणनखण्ड है |
अतः 3x2−5 भी बहुपद f(x) का एक गुणनखण्ड है |
अब f(x) को 3x2−5 से विभाजित करते है |
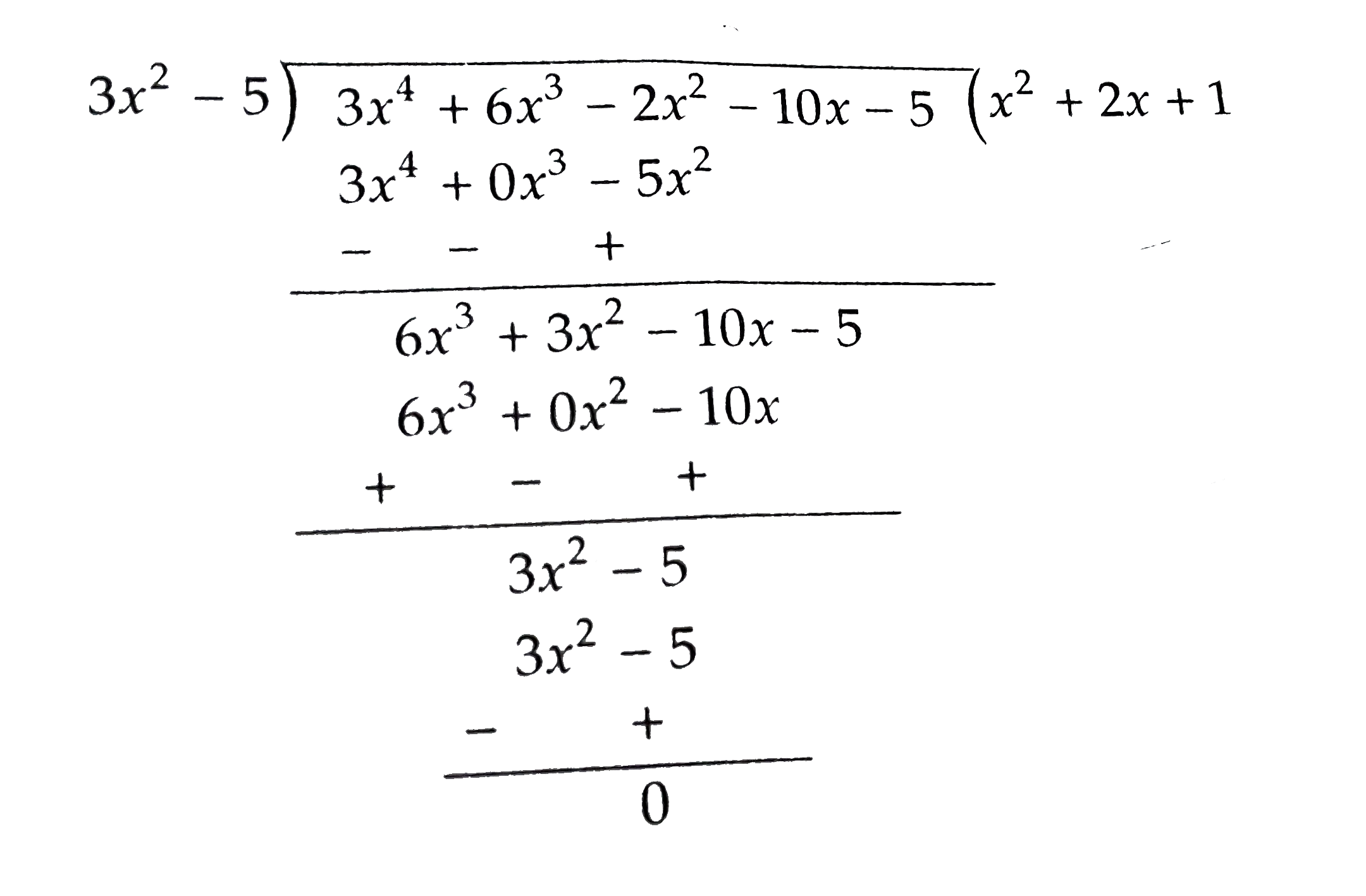
विभाजन एल्गोरिथ्म से,
3x4+6x3−2x2−10x−5=(3x2−5)(x2+2x+1)
⇒3x4+6x3−2x2−10x−5=(√3x+√5)(√3x−√5)(x+1)2
अतः बहुपद f(x) के शून्यक −√53,√53,−1 और −1 है |
|
Similar Questions
बहुपद|बहुपद के प्रकार|शून्यक|किसी बहुपद के शून्यकों और गुणांकों में सम्बन्ध|अभ्यास कार्य|सारांश
View Solutionबहुपद|बहुपद के शून्यक#!#महत्वपूर्ण प्रश्न
View Solutionबहुपद के शून्यक
View Solutionबहुपद की घात#!#बहुपद के प्रकार#!#बहुपद के शून्यक
View Solutionबहुपद के शून्यक#!#शून्यक के ज्यामितीय रूप
View Solutionबहुपद के शून्यक
View Solutionबहुपद के शून्यक#!#शेषफल प्रमेय
View Solutionबहुपद#!#बहुपद का शून्यक
View Solution