यदि बहुपद f(x)=x4−6x3−26x2+138x−35 के दो शून्यक 2±√3 है, तो अन्य शून्यक ज्ञात कीजिये |
वीडियो समाधान
लिखित उत्तर
चूँकि 2+√3 और 2−√3 बहुपद f(x) के दो शून्यक है |
∴{x−(2+√3)}{x−(2−√3)}
=(x−2−√3)(x−2+√3)
=(x−2)2−(√3)2=x2−4x+1,f(x) का एक गुणनखण्ड है |
अतः बहुपद f(x) को x2−4x+1 से विभाजित करते है |
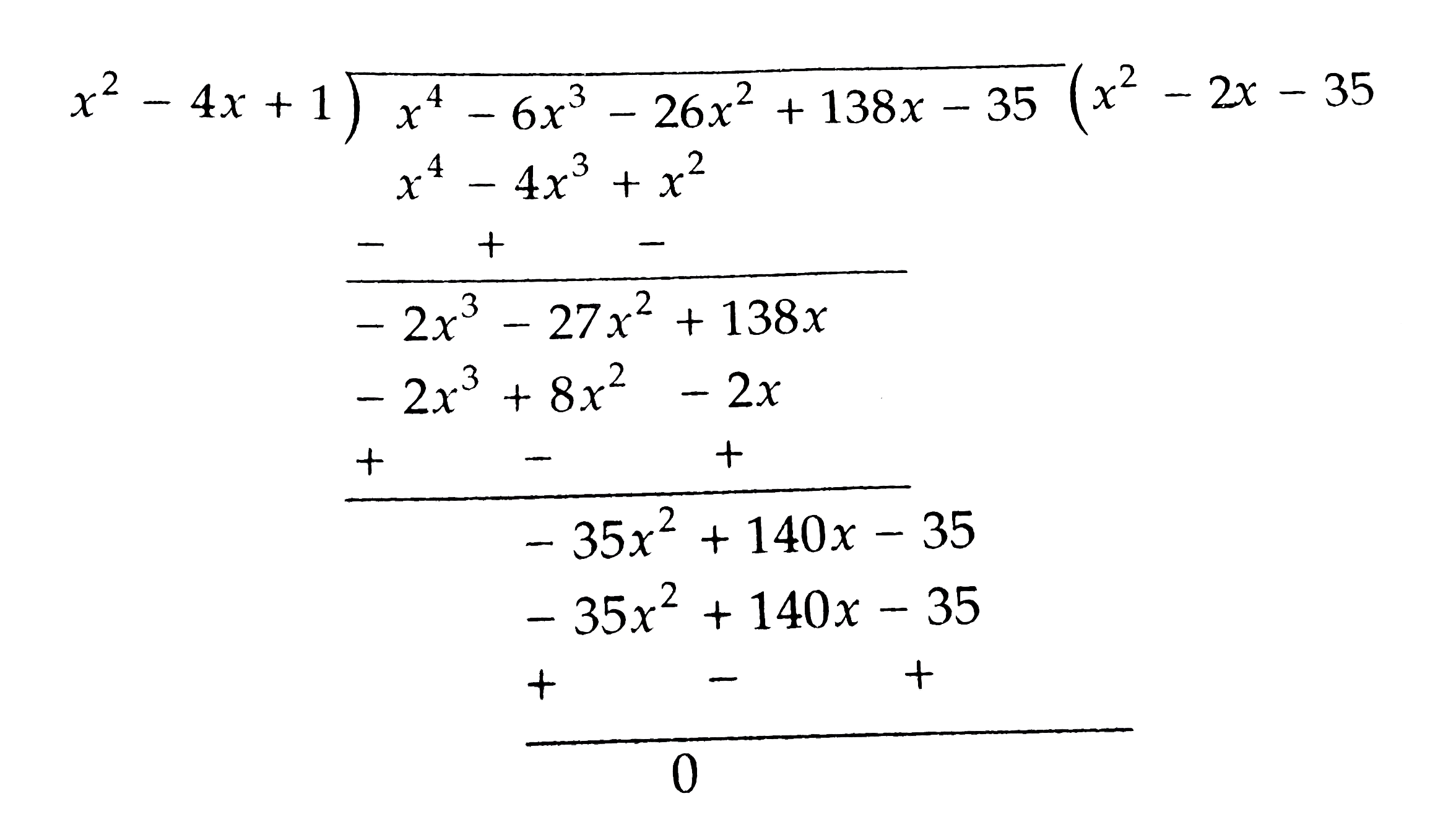
∴f(x)=(x2−4x+1)(x2−2x−35)
अतः बहुपद f(x) के अन्य शून्यक बहुपद x2−2x−35 के शून्यक है |
∵x2−2x−35=x2−7x+5x−35=(x−7)(x+5)
अतः f(x) के अन्य दो शून्यक 7 और -5 है |
|
समान प्रश्न
If two zeroes of the polynomial x4−6x3−26x2+138x−35are 2±√3, find other zeroes.
View SolutionRevision|बहुपद#!#बहुपद के शून्यक#!#ज्यामितीय अर्थ
View SolutionIf two zeros of the polynomial f(x)=x4−6x3−26x2+138x−35 are 2±√3 , find other zeros.
View Solutionबहुपद|बहुपदों के प्रकार|बहुपद के शून्यक|बहुपद के शून्यक का जयमितीय अर्थ|अभ्यास कार्य|सारांश
View Solutionबहुपद|बहुपद के शून्यक#!#महत्वपूर्ण प्रश्न
View Solutionबहुपद के शून्यक
View Solutionबहुपद की घात#!#बहुपद के प्रकार#!#बहुपद के शून्यक
View Solutionबहुपद के शून्यक#!#शून्यक के ज्यामितीय रूप
View Solution
