यदि बिन्दु (3,4) समीकरण 3y=ax+7 के आलेख पर स्थित हो, तो a का मान ज्ञात करो ।
वीडियो समाधान
लिखित उत्तर
चूँकि एक रैखिक समीकरण के आलेख पर प्रत्येक बिन्दु उस समीकरण का एक हल होता है। इसलिए x=3 तथा y=4 समीकरण 3y=ax+7 का एक हल है ।
∴3×4=a×3+7
⇒12=3a+7⇒3a=5⇒a=53
|
समान प्रश्न
यदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionयदि समीकरण x2−bxax−c=m−1m+1 के मूल बारबार व् विपरीत चिन्हो के हो, तो m का मान होगा
View Solutionयदि समीकरण x2+2mx+m2−2m+6=0 के मूल बराबर हो, तो m का मान होगा।
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionयदि α,β वर्ग समीकरण 4x2+3x+7=0 के मूल हो, तो 1α+1β का मान ज्ञात कीजिए।
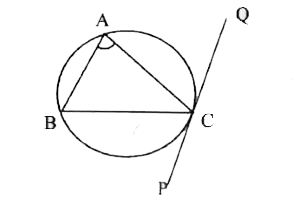
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP ज्ञात करो।
View Solutionयदि a=9−4√5 हो तो √a−1√a एवं a2+1a2का मान ज्ञात करे
View Solution
