त्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
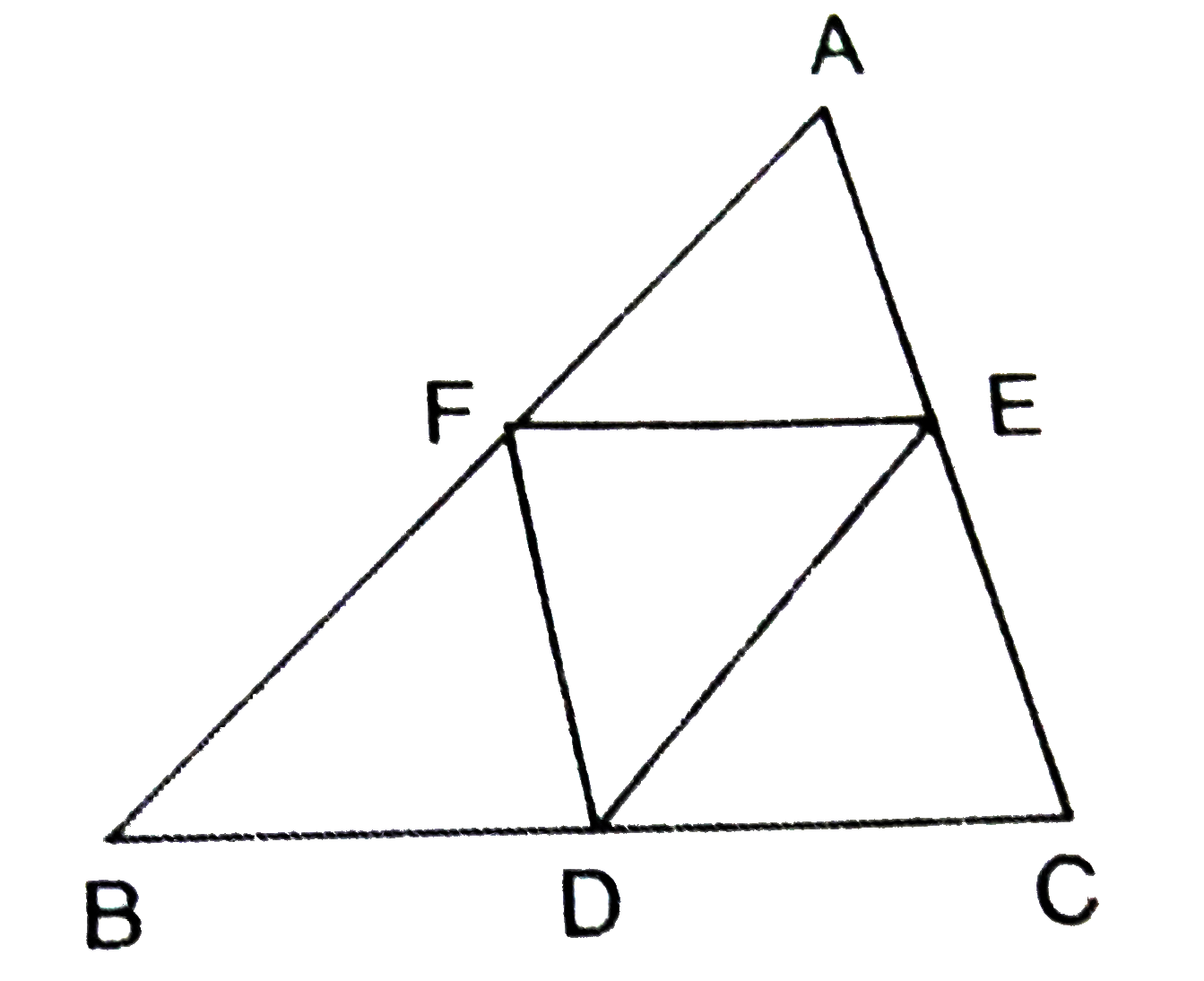
चूँकि भुजाओं BC तथा AC के मध्य-बिंदु क्रमशः D तथा E है।
∴DE||BA⇒DE||BF
इसी प्रकार FE||BD. अतः BDEF एक समांतर चतुर्भुज है। इसी प्रकार DCEF तथा AFDE समांतर चतुर्भुज है।
चूँकि ||gmBDEF का विकर्ण DF है।
∴ar(ΔBDF)=ar(ΔDEF) ...(i)
||gm DCEF का विकर्ण DE है।
∴ar(ΔDCE)=ar(ΔDEF) ...(ii)
||gm AFDE का विकर्ण FE है।
∴ar(ΔAFE)=ar(ΔDEF) ...(iii)
(i), (ii) तथा (iii) से
ar(ΔBDF)=ar(ΔDCE)=ar(ΔAFE)=ar(ΔDEF)
परन्तु ar(ΔBDF)+ar(ΔDCE)+ar(ΔAFE)+ar(ΔDEF)=ar(ΔABC)
∴4ar(ΔDEF)=ar(ΔABC)
⇒ar(ΔDEF)=14ar(ΔABC)
अब ar(||gmBDEF)=2ar(ΔDEF)
⇒ar(||gmBDEF)=2×14ar(ΔABC)=12ar(ΔABC)
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
निम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
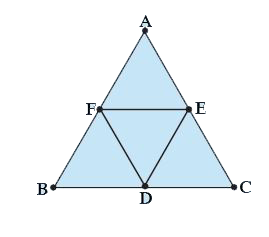
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
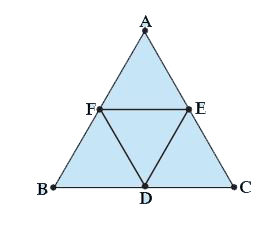
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionIf ΔABC and ΔDEF are two tnangles such that ABEF=BCFD=CADE=34 then find ar(ΔDEF):ar(ΔABC).
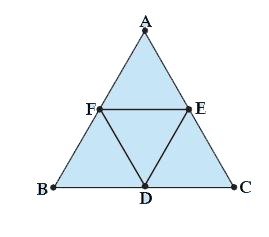
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionD, E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ BC,CA ਅਤੇ AB ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ।ਦਰਸਾਉ ਕਿ:- ar(BDEF)=12ar(ABC)
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View Solution