ABCD एक समांतर चतुर्भुज है भुजाओं BC तथा CD के मध्य-बिंदु क्रमशः X तथा Y है। सिद्ध कीजिए कि ar(ΔAXY)=38ar(।।gmABCD)
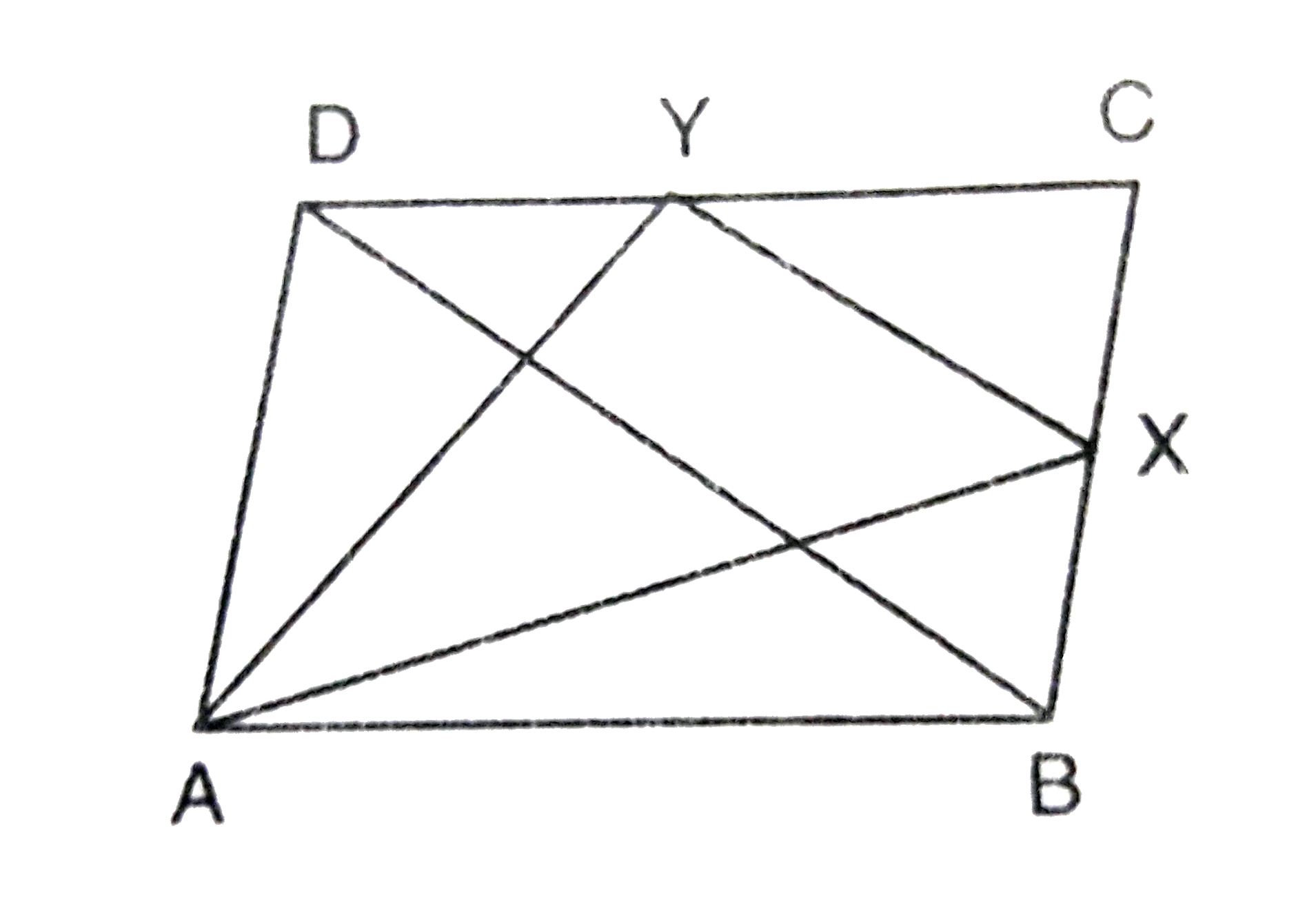
दिया है : एक समांतर चतुर्भुज ABCD जिसमें भुजाओं BC तथा CD के मध्य-बिंदु क्रमशः X तथा Y है।
सिद्ध करना है : ar(ΔAXY)=38ar(||gmABCD).
रचना: BD को मिलाइये।
उपपत्ति: चूँकि ΔABCD में भुजाओं BC तथा CD के मध्य-बिंदु क्रमशः X तथा Y है।
∴XY ||BD तथा XY=12BD
⇒ar(ΔCYX)=14ar(ΔDBC)
=18ar(||gmABCD) [∵12ar(||gmABCD)=ar(ΔBCD)] ...(i)
चूँकि समांतर चतुर्भुज ABCD तथा ΔABX समान रेखाएँ AD तथा BD के बीच स्थित है, तथा
BX=12BC
∴ar(ΔABX)=14ar(||gmABCD) ...(ii)
इसी प्रकार, ar(ΔAYD)=14ar(||gmABCD) ...(iii)
(i ) , (ii ) तथा (iii ) से
ar(ΔAXY)=ar(||gmABCD)−[ar(ΔABX)+ar(ΔAYD)+ar(ΔCYX)]
=ar(||gmABCD)−(14+14+18)ar(||gmABCD)
=(1−58)ar(||gmABCD)=38ar(||gmABCD)
Topper's Solved these Questions
Similar Questions
निम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View SolutionABCD is parallelogram. X and Y are the mid-points of BC and CD respectively. Prove that ar (ΔAXY)=38 ar (∣∣gmABCD).
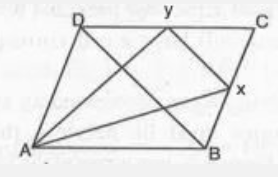
View SolutionGiven a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionABCD is a trapezium with AD and BC parallel sides. E is a point on BC. The ratio of the area trapezium ABCD to that of triangle AED is- ABCD एक AD और BC समांतर भुजाओं वाला समलंब चतुर्भुज है। E,BC पर एक बिंदु है। square ABCD और triangle AED के क्षेत्रफल का अनुपात क्या होगा?
View Solution
