Two block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velicity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
(a) Let T be the tansion in the string. Then,
2T=20t
T=20t newton
Let the block A loses its contact with the floor at time t=t1. This happens when the tension in string becomes equal to the weight of A . Thus,
T=mg
or 10t2=1×10
or t2=1s ...(i)
Similarly, for block B we have
10t2=2×10
or t2=2s ...(ii)
i.e. the block B loses contact at 2s. For block A, at time t such that t≥t1 let a be its acceleration in upward direction.Then,
10t−1×10=1×a=(dv/dt)
du=10(t−1)dt ...(iii)
Integrating this expression, we get
∫v0dv=10∫t1(t−1)dt
or v=5t2−10t+5 ...(iv)
Substituting t=t2=2s
v=20−20+5=5m/s ...(v)
(b) From Eq. (iv). dy=(5t2−10t+5)dt ...(vi)
when, y is the vertical displacement of block A at time t(≥t1). Integrating, we have
∫y=hy=0=∫t=2t=1(5t2−10t+5)dt
h=5[t33]21−10[t22]21+5[t]21=53m
:. Height raised by pulley upto that instant =h2=56m
Similar Questions
Two blocks A and B having masses m1=1kgm2=4kg are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is 4/x sec then x is:
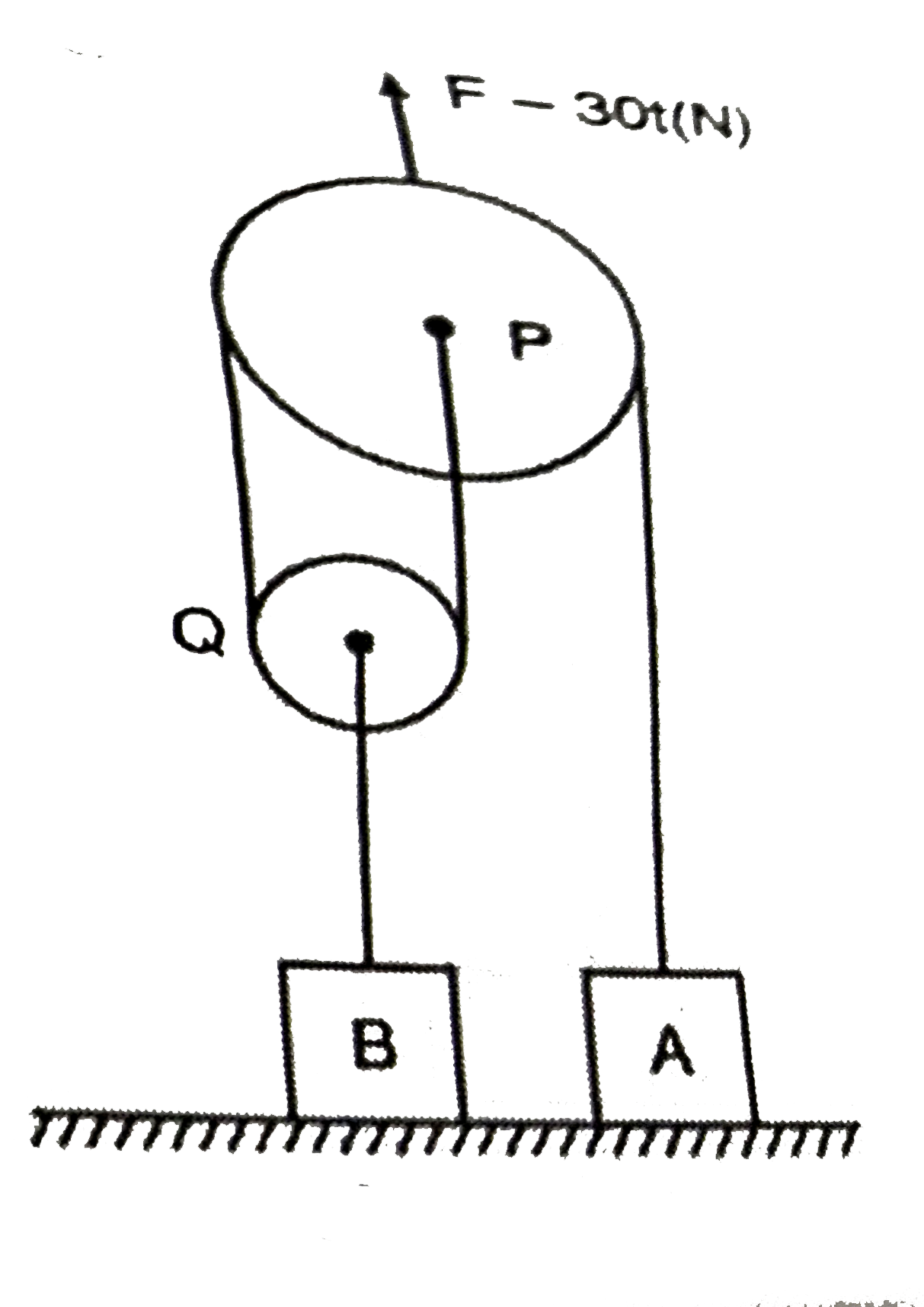
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionString going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.

View SolutionTwo bodies of masses 6 kg and 4 kg respectively are connected to two ends of a light string passing over horizontal frictionless pulley. The acceleration in the string is :
View SolutionTwo blocks A & B are connected by the massless string & pulley. As the blocks are left to move, the force by the pulley on the clamp is
View SolutionTwo blocks of masses 2kg and 5kg are at rest on ground. The masses are connected by a string passing over a frictionless pulley which is under the influence of a constant upward force F = 50 N. Find the accelerations of 5kg and 2kg masses.
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View Solution

