A heavy partile slides under gravity download the inside of a smooth vertical tube dheld in vertical plane. It starts from the highest point with velocity √2ag , where a is the radius of the circle. Find the angular position θ (as shown in figure) at which the vertical acceleration of the particle is maximum.
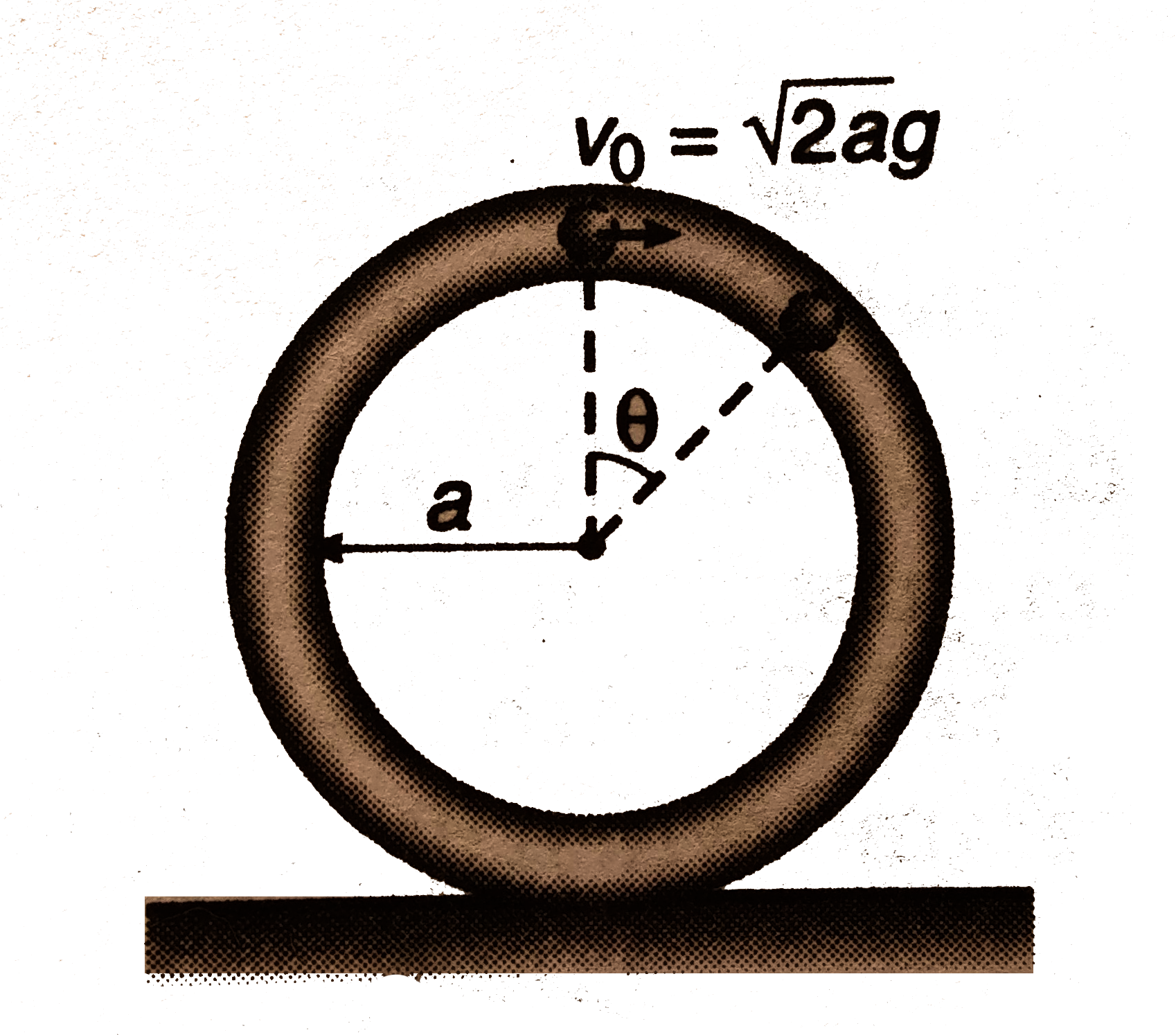
The correct Answer is:A, B, C
At position θ ,
v2=v20+2gh
where, h=a(1−cosθ)
:. v2=(√2ag)2+2ag(1−cosθ)
or v2=2ag(2−cosθ) ...(i)
N+mgcosθ=mv2a
or N+mgcosθ=2mg(2−cosθ)
or N=mg(4−3cosθ)
Net vertical force,
F=Ncosθ+mg
=mg(4cosθ−3cos2θ+1)
This force (or acceleration) will maximum when dFdthη=0
or −4sinθ+6sinθcos=0
So, either
sinθ=0 ,
θ=0∘ ,
or cosθ=23 ,
θ=cos−1(23)
θ=0∘ is unacceptable
Therefore, the desired position is at
θcos−1(23)
Similar Questions
A particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
View SolutionA particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
View Solution
Knowledge Check
A particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
AR2BRC2RD5R4A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
A1:6B1:4C1:3D1:2A particle is projected under gravity with velocity √2ag from a point at a height h above the level plane at an angle θ to it. The maximum range R on the grond is :
A√(a2+1)/hB√(a2h)C√(ah)D2√a(a+h)
The time a body takes to slide down any smooth chord of a vertical circle, which is drawn from the highest point of the circle is constant.
View SolutionA body tied at the end of a string of length ' l' is rotated on a vertical circle. The velocity of the body at the highest point is √2gl .The maximum velocity of the body would be
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View SolutionA particle starts rotating from rest according to the formula θ=(t2/64)−(t/8) where θ is the angle in radian and t in s . Find the angular velocity and angular acceleration at the end of 4 s .
View Solution

