A rocket of initial mass m0 has a mass m0(1−t/3) at time t. The rocket is lauched from rest vertically upwards under gravity and expels burnt fuel at a speed u relative to the rocket vertically downward. Find the speed of rocket at t=1.
The correct Answer is:B, C
(−dmdt)=m03
At t=1, mass will remain,
m=m0−m03=23m0
Now using the equation,
v=u−gt+vr1n(m0m)
=0−g(1)+u1n(m02/3m0)
=u1n(32)−g
Similar Questions
A rocket with an initial mass of 1000kg, is launched vertically upward from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000m/s relative to the rocket . Find the velocity of the rocket after 1min of start.
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
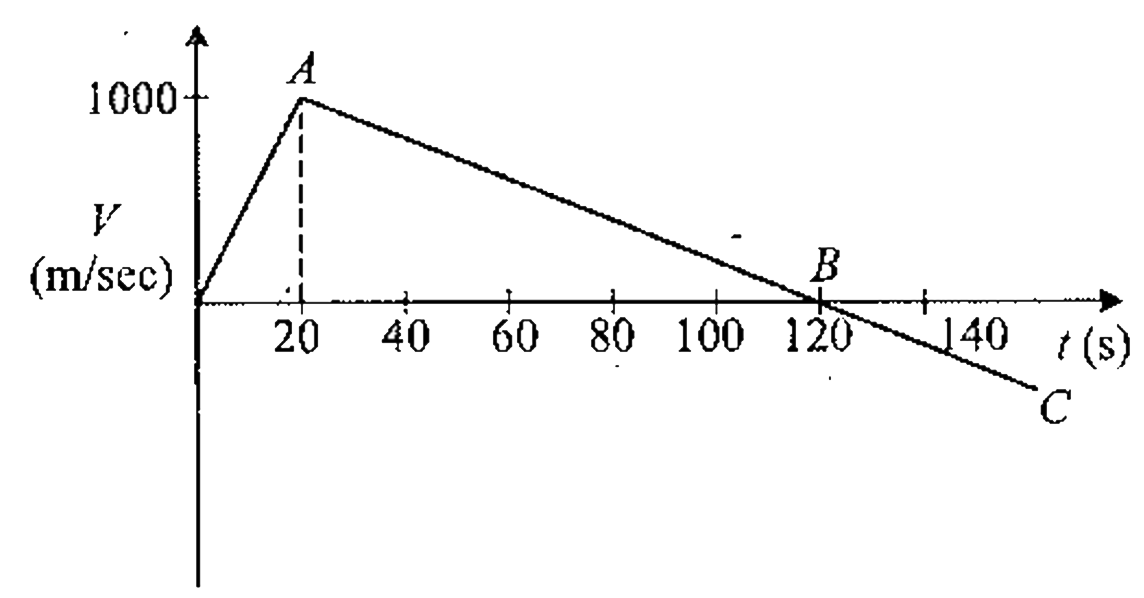
View Solution
Knowledge Check
A rocket, with an initial mass of 1000kg, is launched vertically upwards from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000ms−1 relative to the rocket. If burning ceases after one minute, find the maximum velocity of the rocket. (Take g as constant at 10ms−2)
A1232.6m//sB123.6m//sC12323.6m//sDNONE OF THE ABOVEA rocket of mass m0 has attained a speed equal to its exhaust speed and that time the mass of the rocket is m. Then the ratio m0m is (neglect gravity)
A(a) 2.718B(b) 7.8C(c) 3.14D(d) 4
A rocket is moving vertically upward against gravity. Its mass at time t is m=m0−μt and it expels burnt fuel at a speed u vertically downward relative to the rocket. Derive the equation of motion of the rocket but do not solve it. Here, μ is constant.
View SolutionA rocket of total mass 1000kg initially is launched from ground. The gases are ejected at the rate 20kg/s with velocity 1000 m/s relative to rocket vertically downwards. The initial acceleration of the rocket is a (in m/s2). Findag. (Take g=10m/s2)
View SolutionA double stage rocket has an initial mass Mi, gas is exhausted front he rocket at a constant rate of dm/dt and with an exhaust velocity u relative to the rocket. When the mass of the rocket reaches the value μ, the first stage of mass m of
Which fuel is exhausted is disengaged from the rocket and then the rocket continues to the second stage at teh same rate and exhaust velocity as int eh first stage, until it reaches a mass Mf
(a). Calculate the rocket velocity at the end of the first stage, given that it is started at rest.
(b). Calculat ethe rocket velocity at the end of the second stage. ltbr> (c). What is the final velocity of a one stage rocket of the same initial Mi mass and the same amount of fuel ? it is greater or less than final velocity of the double stage rocket?
View SolutionA rocket fired from the earth's surface ejects 1% of its mass at a speed of 2000 ms−1 in the first second. Find the average acceleration of the rocket in the first second.
View SolutionConsider a rocket that is in deep space and at rest relative to an inertial reference frame. The rocket's engine is to be fired for a certain interval. What must be the rocket's mass ratio (ratio of initial to final mass) over that interval if the rocket's original speed relative to the inertial frame is to be equal to (a) the exhaust speed (speed of the exhaust products relative to the rocket) and (b) 2.0 times the exhaust speed?
View SolutionA rocket weighs 13,500 kg when fuelled up on the launching pad . It is fired vertically upward . Gases are exhausted at the rate of 145 kg per second with velocity 1500 ms−1 relative to the rocket . What is the thrust on the rocket ?
View Solution
