A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.

(a). Suppose velocity of COM of the rod just after collision is v and angular velocity about is ω is ω. Applying following three laws
(1). External force on the system (rod + mass) in horizontal plane along x-axis is zero
∴ applying conservation of linear momentum in x-direction
mv0=Mv ..(i)
(2). Net torque on the system COM of rod is zero
∴ Applying conservation of angular momentum about COM of rod, we get mv0(L2)=Iω
or mv0L2=ML212ω
or mv0=MLω6 ...(ii)
(3) since, the collision is elastic, kinetic energy is also conserved
∴12mv20=12Mv2+12Iω2
or mv20=Mv2+ML212ω2 ..(iii)
From Eqs (i), (ii) and (iii) we get the following result
mM=14
v=mv0M and ω=6mv0ML
(b). point P will be rest if xω=v
or x=vω=mv0/M6mv0/ML or x=L/6
∴AP=L2+L6 or AP=23L)
(c). After time t=πL3v0
Angle rotated by rod θ=ωt=6mv0ML.πL3v0
=2π(mM)=2π(14)
∴θ=π2
Therefore, situation is as shown in figure
∴resultant velocity of point P will be
|VP|=√2v=√2(mM)v0
=√24v0=v02√2
or |VP|=v02√2


Similar Questions
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses (mM) is 1x. The value of 'x' will be_____.
View Solution
Knowledge Check
A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,
 Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
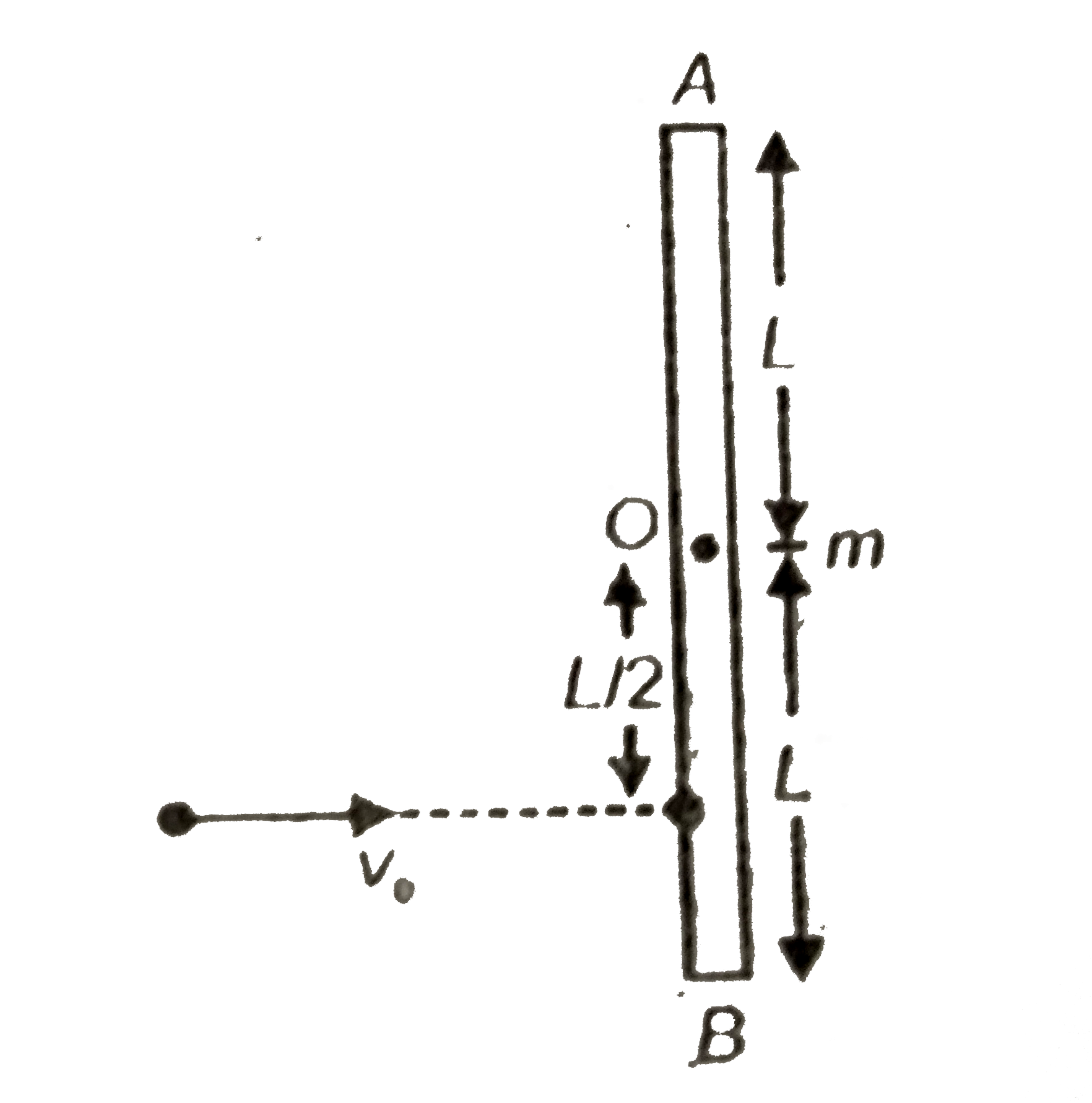
Angular velocity of rod just after collision is
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
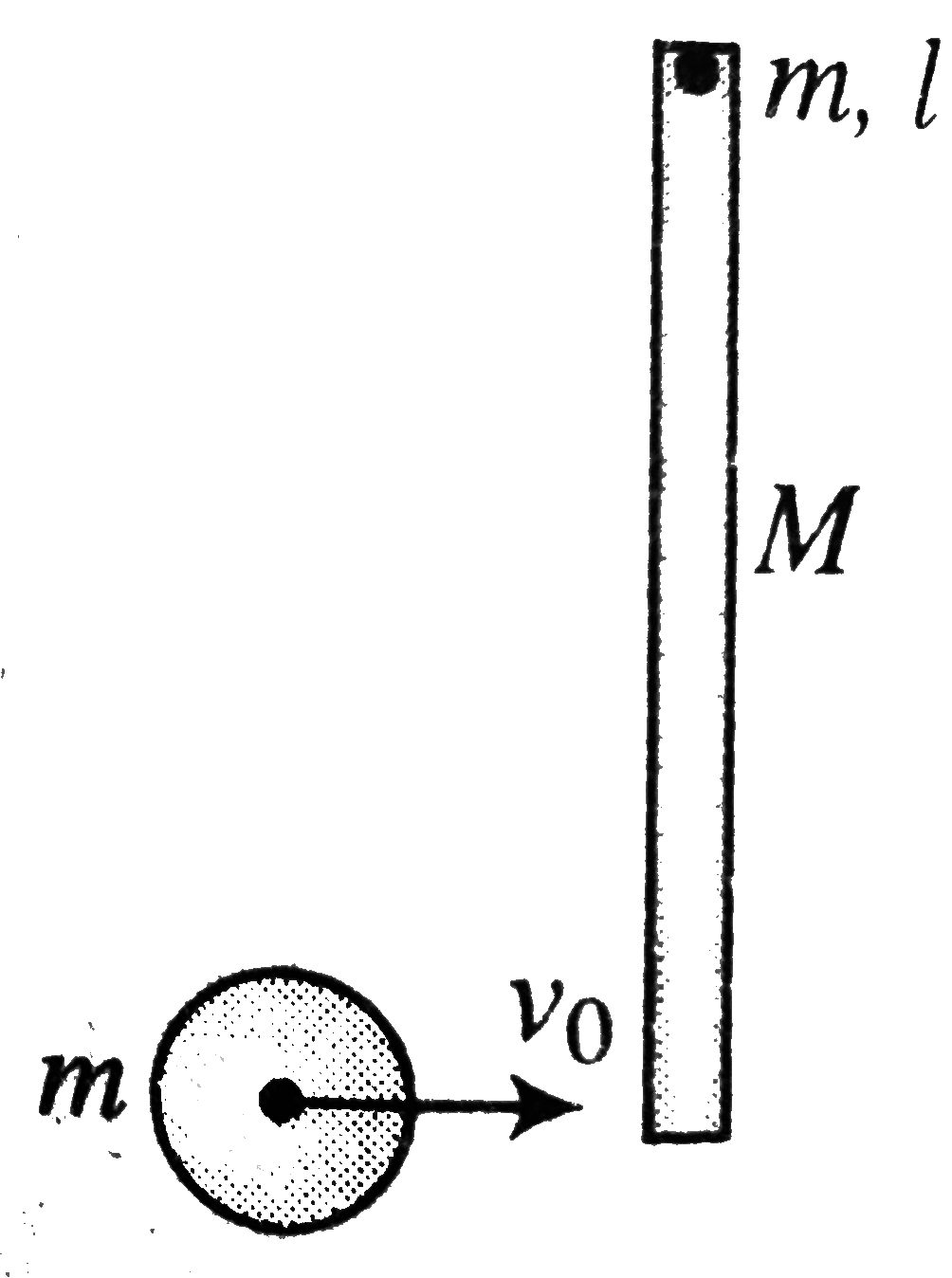
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution
